Lesson 4
- Author:
- Arpit Kesharwani
Dilations on a Square GridLearning goalsLearning goals(Student Facing)Learning targets(Student Facing)Required MaterialsRequired PreparationPrint-Formatted Word DocumentsPrint-Formatted PDFsIn this lesson, students apply dilations to polygons on a grid, both with and without coordinates. The grid offers a way of measuring distances between points, especially points that lie at the intersection of grid lines. If point Q is three grid squares to the right and two grid squares up from P then the dilation with center P of Q with scale factor 4 can be found by counting grid squares: it will be twelve grid squares to the right of P and eight grid squares up from P. The coordinate grid gives a more concise way to describe this dilation. If the center P is (0,0) then Q has coordinates (3,2). The image of Qafter this dilation is (12,8).Students continue to find dilations of polygons, providing additional evidence that dilations map line segments to line segments and hence polygons to polygons. The scale factor of the dilation determines the factor by which the length of those segments increases or decreases. Using coordinates to describe points in the plane helps students develop language for precisely communicating figures in the plane and their images under dilations (MP6). Strategically using coordinates to perform and describe dilations is also a good example of MP7.CCSS Standards: AddressingWARM-UP: 5 minutes4.1: Estimating a Scale FactorCCSS Standards: AddressingIn this warm-up, students estimate a scale factor based on a picture showing the center of the dilation, a point, and its image under the dilation.LaunchTell students they will estimate the scale factor for a dilation. Clarify that “estimate” doesn’t mean “guess.” Encourage students to use any tools available to make a precise estimate. Provide access to geometry toolkits. Student-Facing Task Statement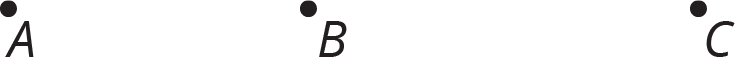
Point C is the dilation of point B with center of dilation A and scale factor s. Estimate s. Be prepared to explain your reasoning. Student ResponseAnswers vary. Sample response: about 2.3. Activity SynthesisCheck with students to find what methods they used to compare distances. Likely methods include using a ruler and division or using an index card and marking off multiples of the distance from A to B.Ask students:
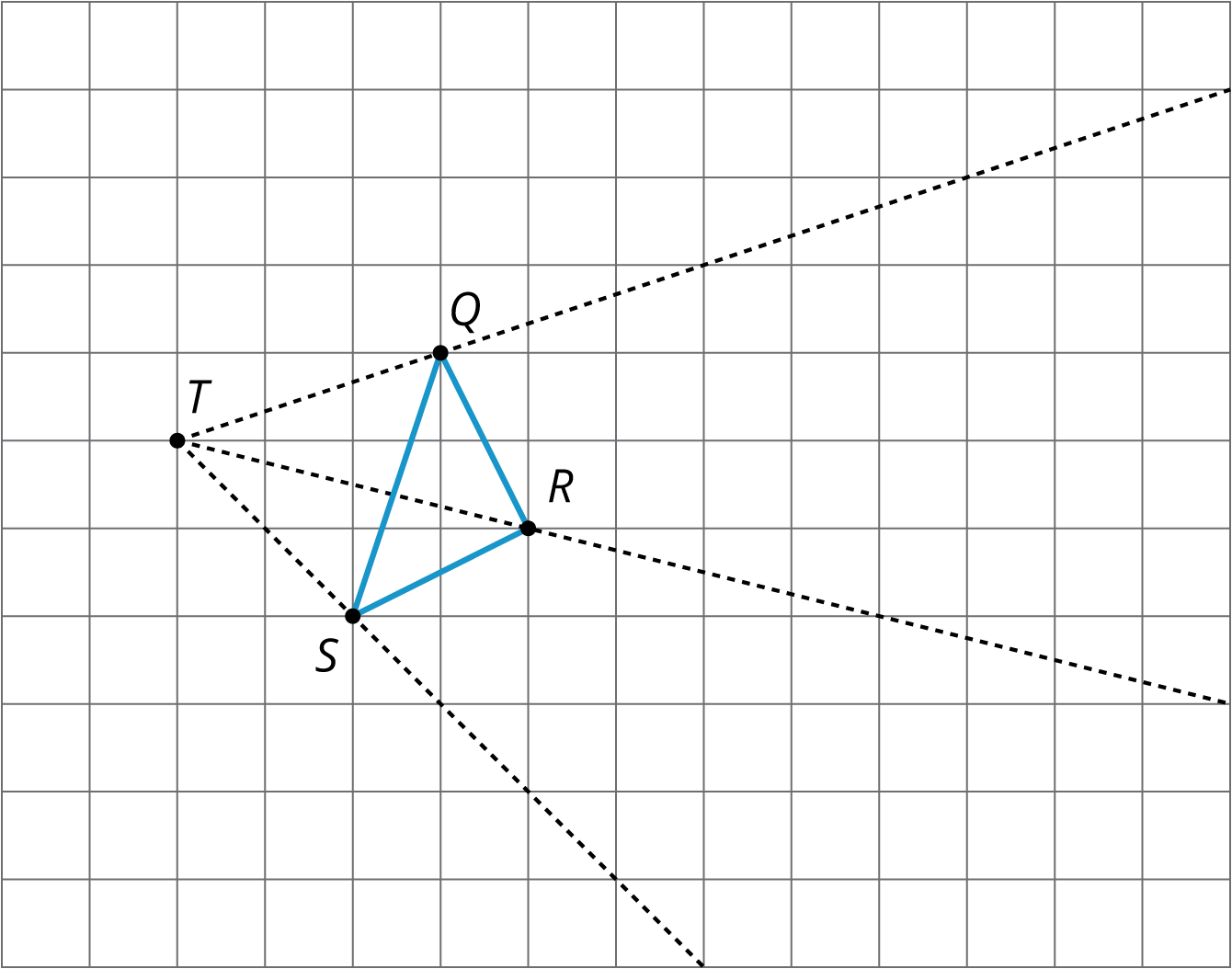Student Response1.
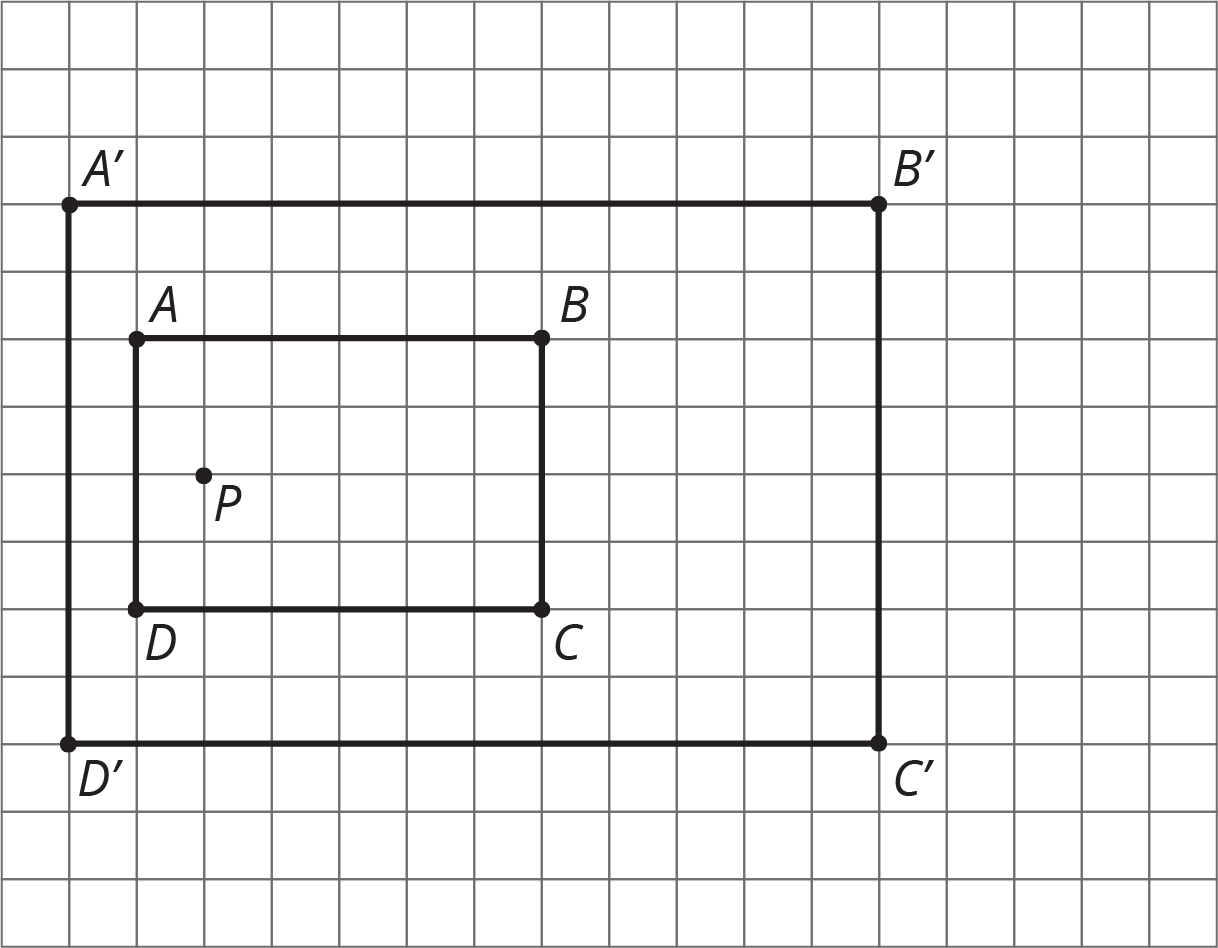2-3.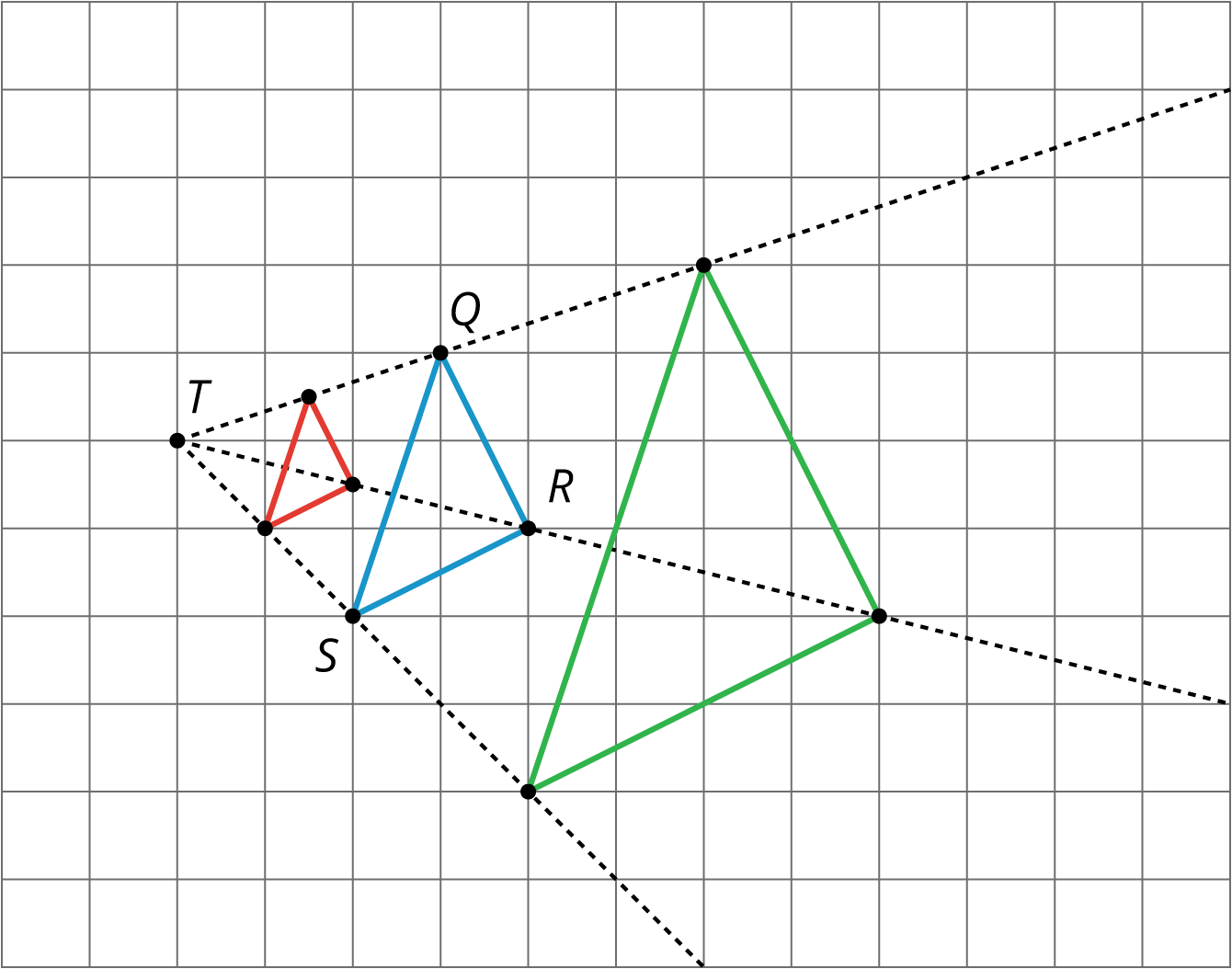
Activity SynthesisSelect students to show how they found the dilations. First, select any students who used the same methods as when there was no grid, followed by students who noticed they could use the structure of the grid. Draw connections between these two methods—show that when you measure with a ruler or by making markings on an index card, the dilated point ends up in the same place as by reasoning about the grid.Expect students to use expressions like “moving over two and up one.” These measurements can be multiplied by the scale factor in order to find the location of the dilated point. Tell students that moving forward they will do work on the grid with the added structure of coordinates. The method of performing dilations is the same. The only change is that the coordinates give a concise way to namepoints. Lighter Support: MLR 8 (Discussion Supports). As students explain their dilation methods and how they relate to scale factor, show central concepts (e.g., grid measurements) multi-modally by using different types of sensory inputs: physically acting out movements (e.g., “over two, up one”), showing the images of the dilations and using gesture to demonstrate the measurements. This promotes the mathematical meaning of the language “scale factor”.ACTIVITY: 15 minutes4.3: Card Sort: Matching Dilations on a Coordinate GridInstructional RoutinesCCSS Standards: AddressingMaterialsIn the previous task, students worked on a square grid without coordinates. This activity adds the structure of coordinates and this extra structure plays a key role, allowing students to name points. Students match figures with their dilated images, using coordinates to describe the center of dilation and the vertices. The same strategies that were used previously in dilating images,on a circular grid and with no grid, will be useful here.Monitor for students who identify that the dilation of a circle is a circle and similarly for triangles and quadrilaterals. This will help them eliminate certain possibilities for each match. Because there is one card that does not match, students should verify the other matches by performing the dilations. Once the card without a match has been identified, reasoning based on eliminating possibilities (without performing the dilations) is correct. Monitor for students who systematically perform the dilations to help identify a match versus those who reason by structure and elimination of possibilities. Invite both to share during the discussion.LaunchStudents practice matching an original figure and dilation description to information about the dilated images using the coordinate plane. Distribute one set (numbers 1 through 6 and letters A through F) of cards to each student.There is one extra option that does not have a match. Students should draw the dilated image for that option themselves. Light Support: MLR 7 (Compare and Connect). After students have completed the task, have them form groups of three. In the groups, each student will pick one match they feel most confident about describing their solution to the other group members. After presenting the solution strategy, the other group members may respond by asking clarifying questions or by sharing their own strategy for that match. It will be useful to model the procedure first for students. Remind students to press each other for details and share any patterns they noticed.Conceptual Processing: Eliminate Barriers. Demonstrate the steps for the activity or game, in which a group of students and staff play an example round while the rest of the class observes.Student-Facing Task StatementYour teacher will give you some cards. Each of Cards 1 through 6 shows a figure in the coordinate plane and describes a dilation.Each of Cards A through E describes the image of the dilation for one of the numbered cards.Match number cards with letter cards. One of the number cards will not have a match. For this card, you’ll need to draw an image.Student Response
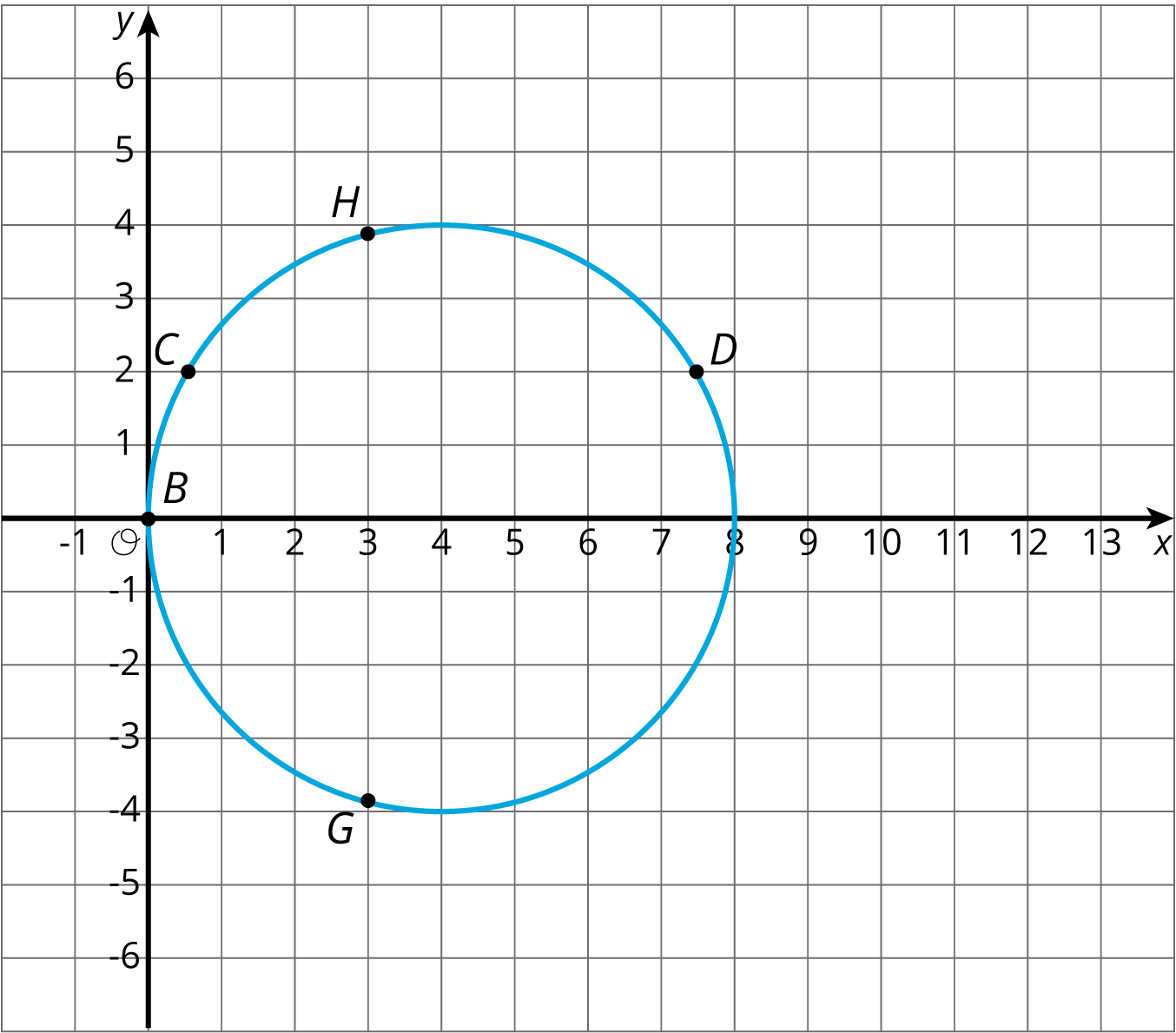"Are you ready for more?" Student ResponseOriginal has center (4,0) and radius 4. Image has center (6,0) and radius 6.
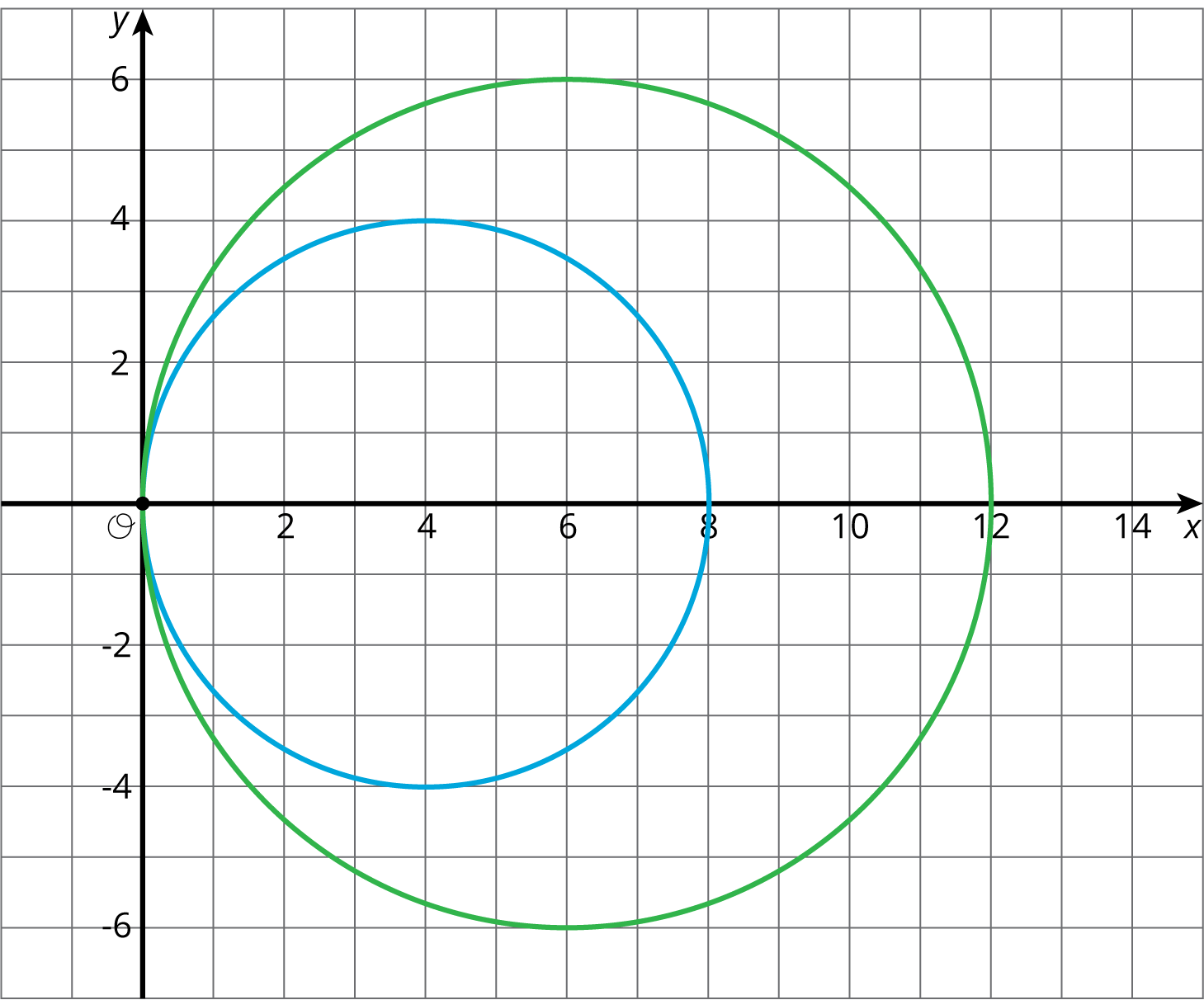Activity SynthesisShare the correct answers and invite selected students to share the strategies they used to solve the problems. This is a matching problem, so students may not have dilated the entire image to find the correct answer among the choices. Important points to bring out include:
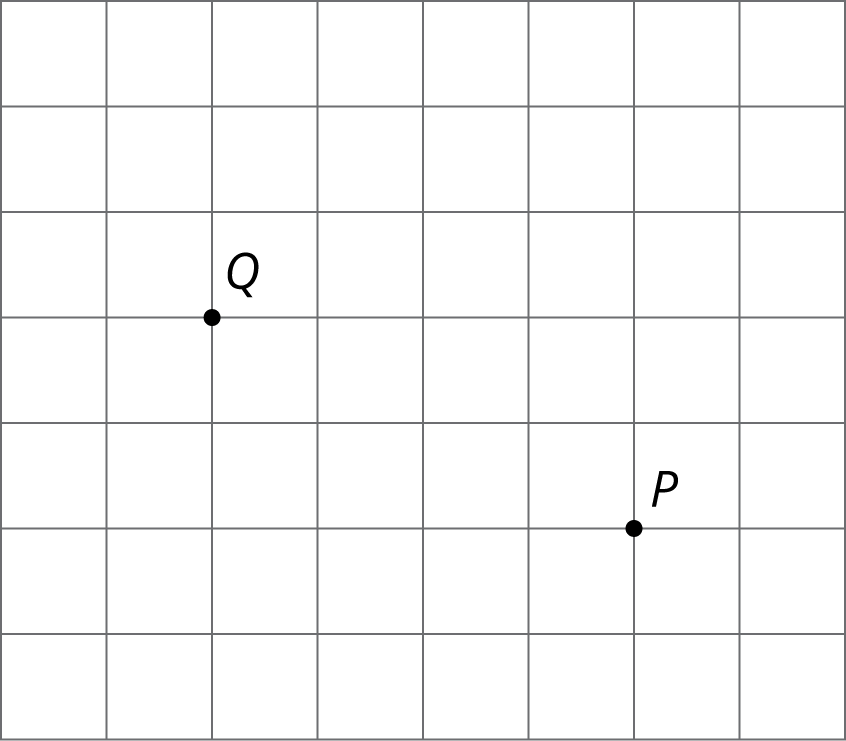The image of Q will be half as many grid lines to the left and half has many grid lines up—that is, 2 grid lines to the left and 1 grid line up from P.When the grid has coordinates, it is easier to communicate the location of new points. In the figure, we have A=(0,0) and B=(2,1).
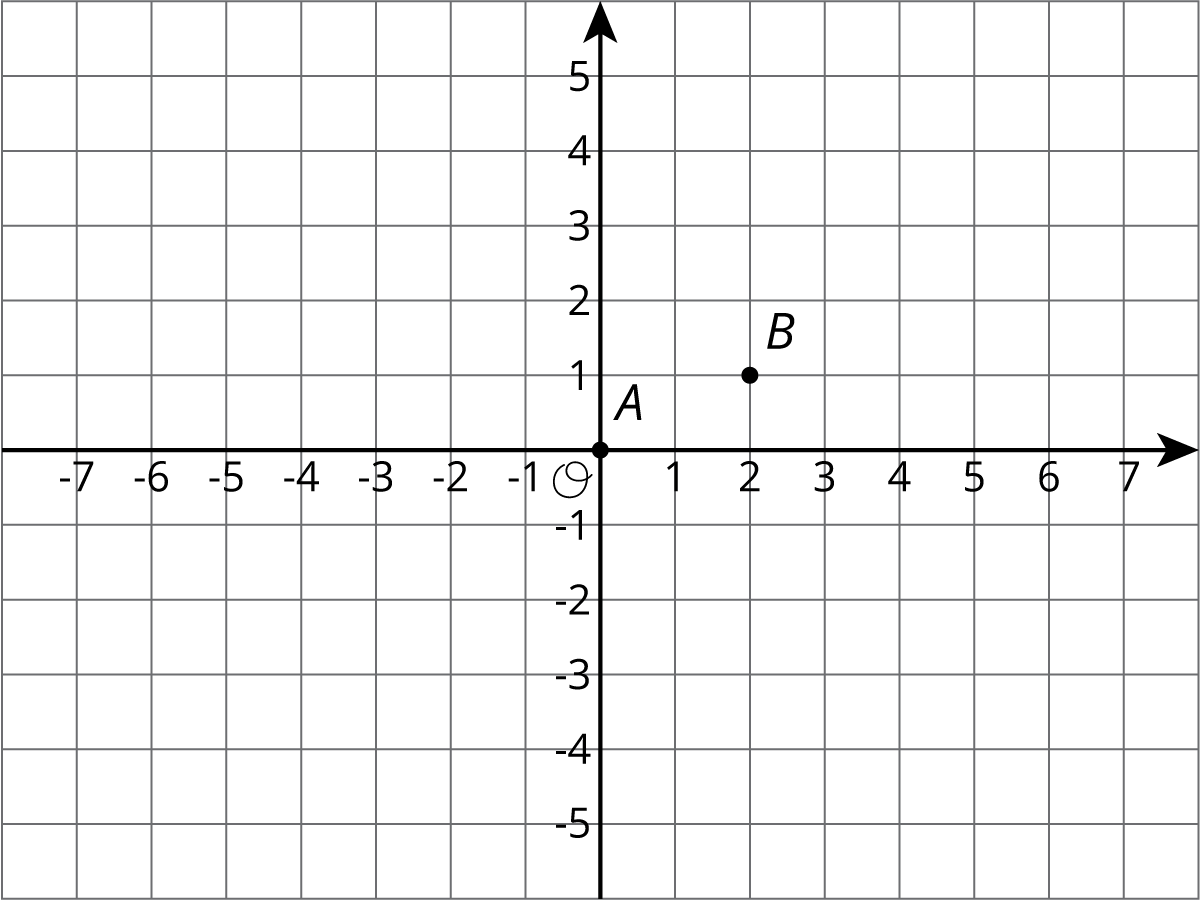What is the dilation of B with center A and scale factor 3? To communicate the answer, we can just say (6,3). It is three times as far to the right and 3 times as far up from A as B so it is the desired point. COOL-DOWN: 5 minutes4.4: A Dilated ImageCCSS Standards: AddressingStudents apply a dilation to a polygon where the center of dilation is on the interior of the figure. The polygon is on a grid without coordinates and the structure of the grid can be efficiently used to find the dilation.Student-Facing Task StatementDraw the image of rectangle ABCD under dilation using center P and scale factor 12.
Student Response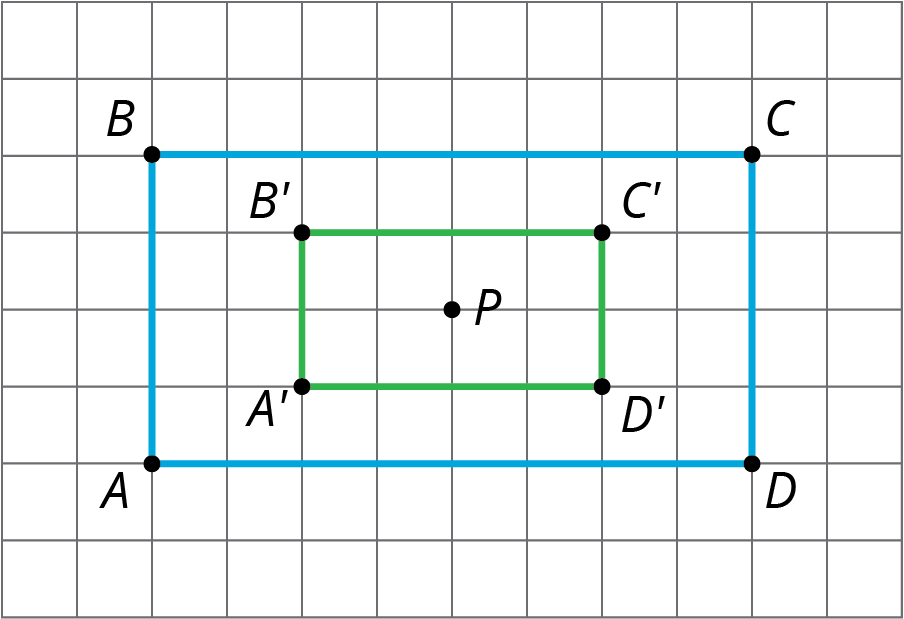
Lesson 3back to topLesson 5Community Created ResourcesCommunity-created resources were developed and submitted by educators using Open Up Resources 6–8 Math curriculum. Thank you to everyone who continues to contribute discussion, resources, and other materials to our community!Coming soon for this lesson.
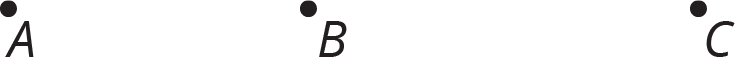Point C is the dilation of point B with center of dilation A and scale factor s. Estimate s. Be prepared to explain your reasoning. Student ResponseAnswers vary. Sample response: about 2.3. Activity SynthesisCheck with students to find what methods they used to compare distances. Likely methods include using a ruler and division or using an index card and marking off multiples of the distance from A to B.Ask students:- “Is the scale factor greater than 1?” (Yes.) “How do you know?” (the point C is further from A than B)
- “Is the scale factor greater than 2?” (Yes.) “How do you know?” (the distance from C to A is more than twice the distance from B to A)
- “Is the scale factor greater than 3?” (No.) “How do you know?” (The distance from C to A is less than 3 times the distance from B to A.)
- “Is the scale factor greater or less than 2.5?” (It is less.) “How do you know?” (The distance from C to A is less than 2.5 times the distance from B to A.)
- using a ruler or index card to measure distances along the rays emanating from the center of dilation
- taking advantage of the grid and counting how many squares to the left or right, up or down
- Find the dilation of quadrilateral ABCD with center P and scale factor 2.
- Find the dilation of triangle QRS with center T and scale factor 2.
- Find the dilation of triangle QRS with center T and scale factor 12.
Student Response1.2-3.Activity SynthesisSelect students to show how they found the dilations. First, select any students who used the same methods as when there was no grid, followed by students who noticed they could use the structure of the grid. Draw connections between these two methods—show that when you measure with a ruler or by making markings on an index card, the dilated point ends up in the same place as by reasoning about the grid.Expect students to use expressions like “moving over two and up one.” These measurements can be multiplied by the scale factor in order to find the location of the dilated point. Tell students that moving forward they will do work on the grid with the added structure of coordinates. The method of performing dilations is the same. The only change is that the coordinates give a concise way to namepoints. Lighter Support: MLR 8 (Discussion Supports). As students explain their dilation methods and how they relate to scale factor, show central concepts (e.g., grid measurements) multi-modally by using different types of sensory inputs: physically acting out movements (e.g., “over two, up one”), showing the images of the dilations and using gesture to demonstrate the measurements. This promotes the mathematical meaning of the language “scale factor”.ACTIVITY: 15 minutes4.3: Card Sort: Matching Dilations on a Coordinate GridInstructional RoutinesCCSS Standards: AddressingMaterialsIn the previous task, students worked on a square grid without coordinates. This activity adds the structure of coordinates and this extra structure plays a key role, allowing students to name points. Students match figures with their dilated images, using coordinates to describe the center of dilation and the vertices. The same strategies that were used previously in dilating images,on a circular grid and with no grid, will be useful here.Monitor for students who identify that the dilation of a circle is a circle and similarly for triangles and quadrilaterals. This will help them eliminate certain possibilities for each match. Because there is one card that does not match, students should verify the other matches by performing the dilations. Once the card without a match has been identified, reasoning based on eliminating possibilities (without performing the dilations) is correct. Monitor for students who systematically perform the dilations to help identify a match versus those who reason by structure and elimination of possibilities. Invite both to share during the discussion.LaunchStudents practice matching an original figure and dilation description to information about the dilated images using the coordinate plane. Distribute one set (numbers 1 through 6 and letters A through F) of cards to each student.There is one extra option that does not have a match. Students should draw the dilated image for that option themselves. Light Support: MLR 7 (Compare and Connect). After students have completed the task, have them form groups of three. In the groups, each student will pick one match they feel most confident about describing their solution to the other group members. After presenting the solution strategy, the other group members may respond by asking clarifying questions or by sharing their own strategy for that match. It will be useful to model the procedure first for students. Remind students to press each other for details and share any patterns they noticed.Conceptual Processing: Eliminate Barriers. Demonstrate the steps for the activity or game, in which a group of students and staff play an example round while the rest of the class observes.Student-Facing Task StatementYour teacher will give you some cards. Each of Cards 1 through 6 shows a figure in the coordinate plane and describes a dilation.Each of Cards A through E describes the image of the dilation for one of the numbered cards.Match number cards with letter cards. One of the number cards will not have a match. For this card, you’ll need to draw an image.Student Response- C. Answers vary. Sample response: The center of dilation is the point B, so the dilation also contains point B, suggesting this card. The scale factor of 32 works for the two trapezoids which are plotted together.
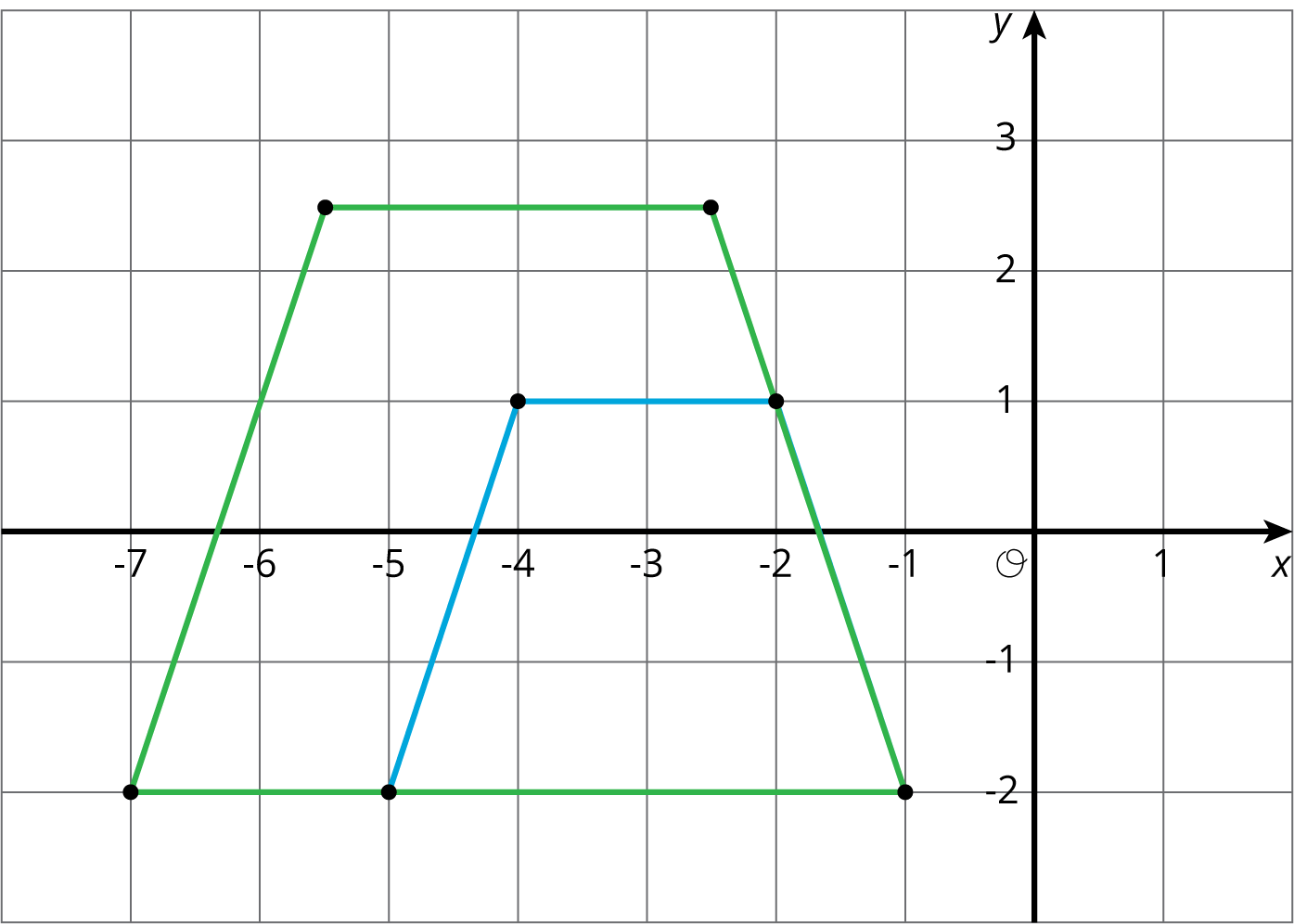
- A. Answers vary. Sample response: The scale factor was less than one, so the dilation will be closer to the center of dilation. Card A is plotted and shows the dilation since each vertex on the green trapezoid is the midpoint between the center of dilation and the corresponding vertex on the blue trapezoid.
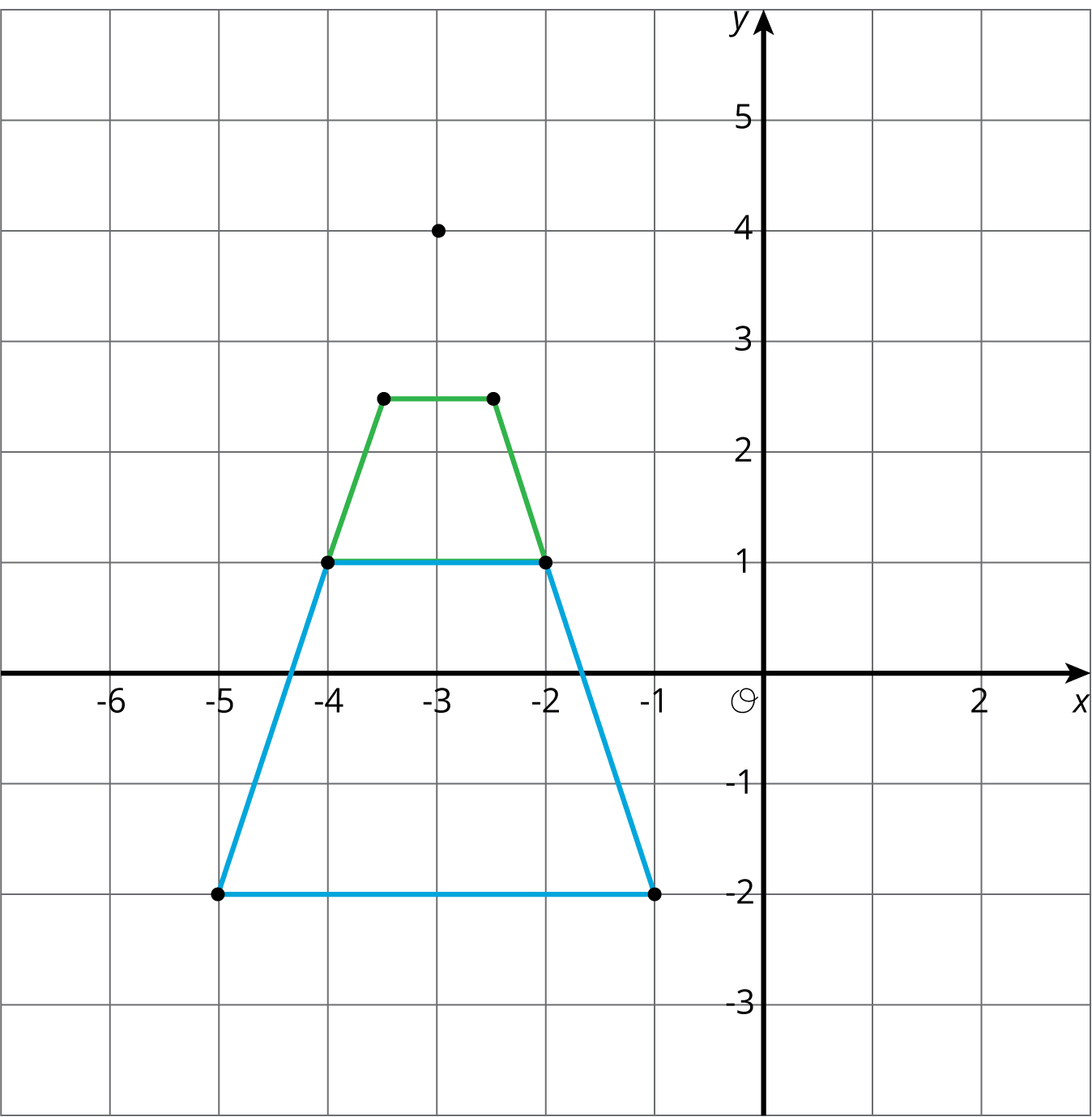
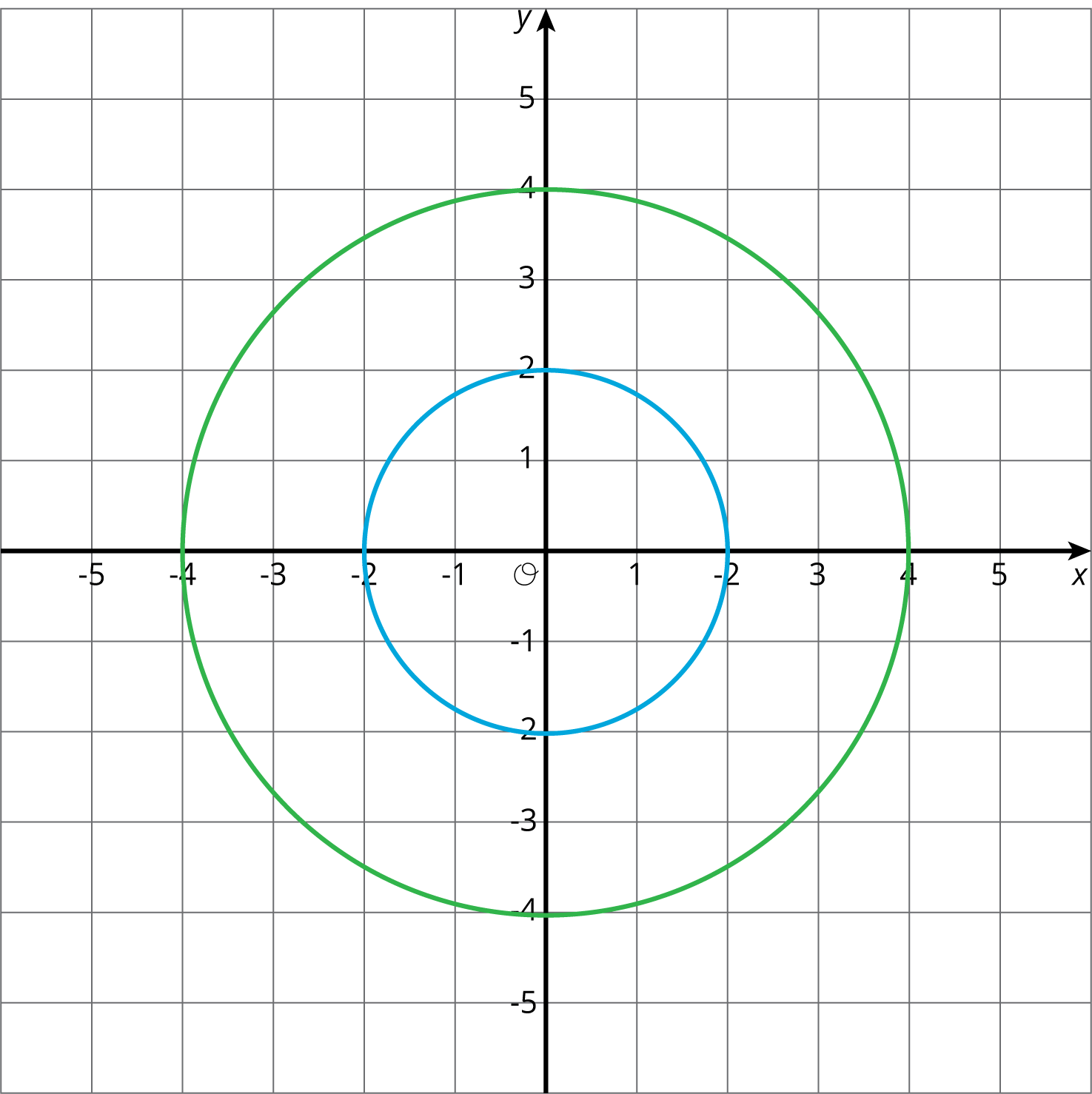
- B. Answers vary. Sample response: The dilation scale factor was greater than one, so the dilated image will be a larger circle. The image is correct as both circles have the same center and the radius of the green circle is twice the radius of the blue circle.
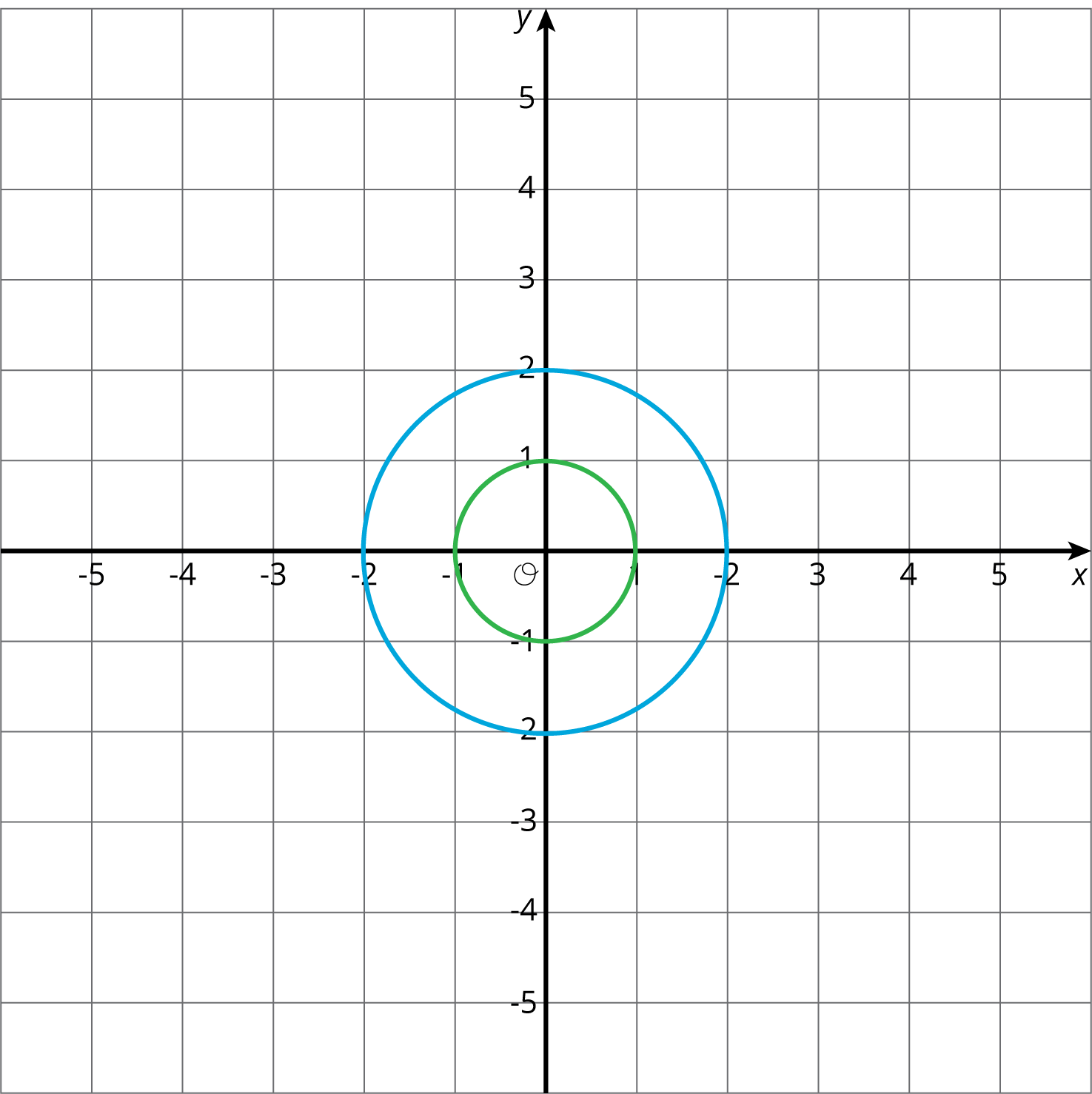
- E. Answers vary. Sample response: This scale factor is less than one, so the image of the dilation is a circle that is smaller than the original one. The image is correct because the circles have the same center and the radius of the green circle is half the radius of the blue circle.
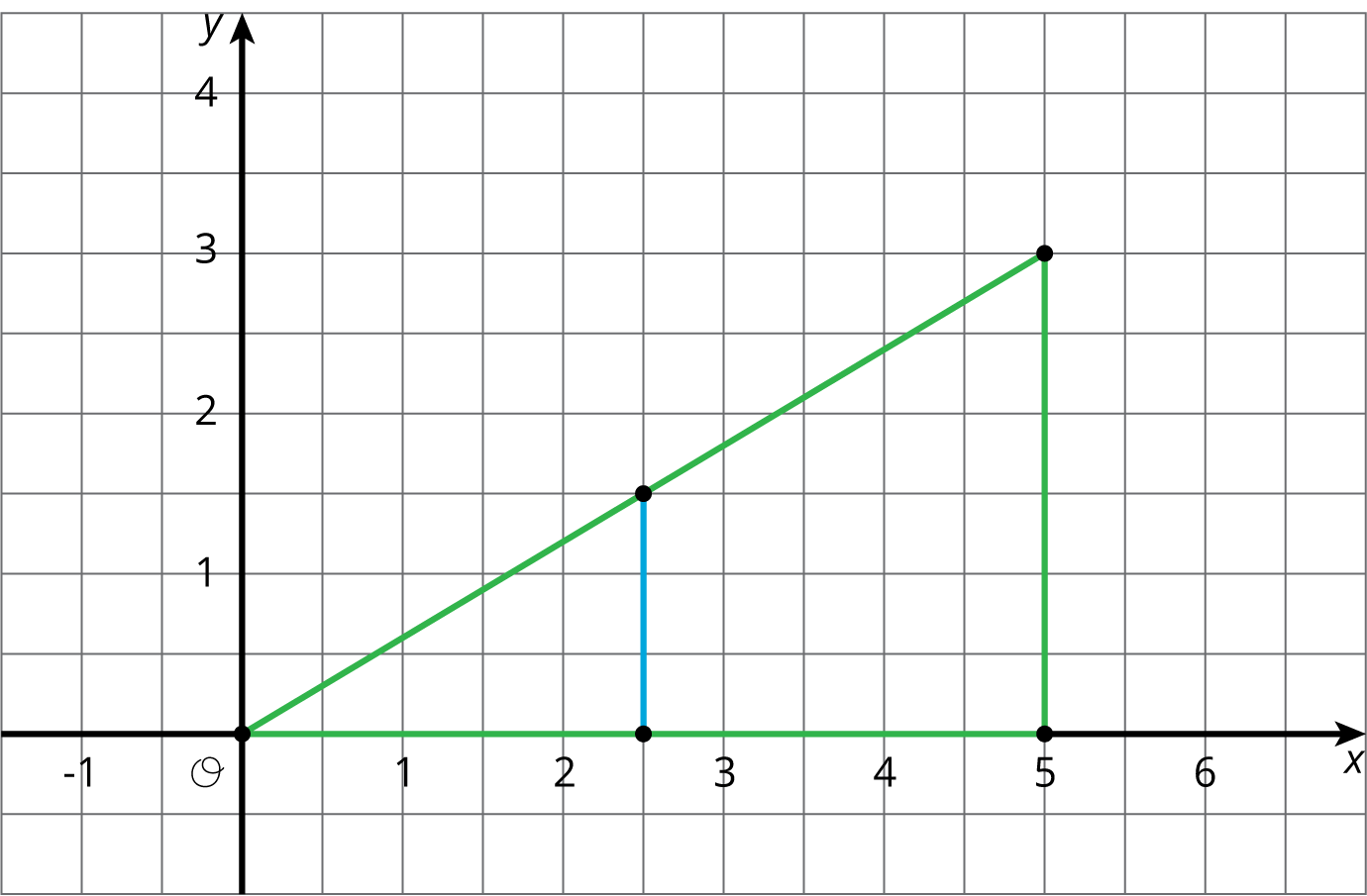
- F. The center of dilation is (0,0) so the dilated image is a triangle containing (0,0). This does not match any of the lettered cards.
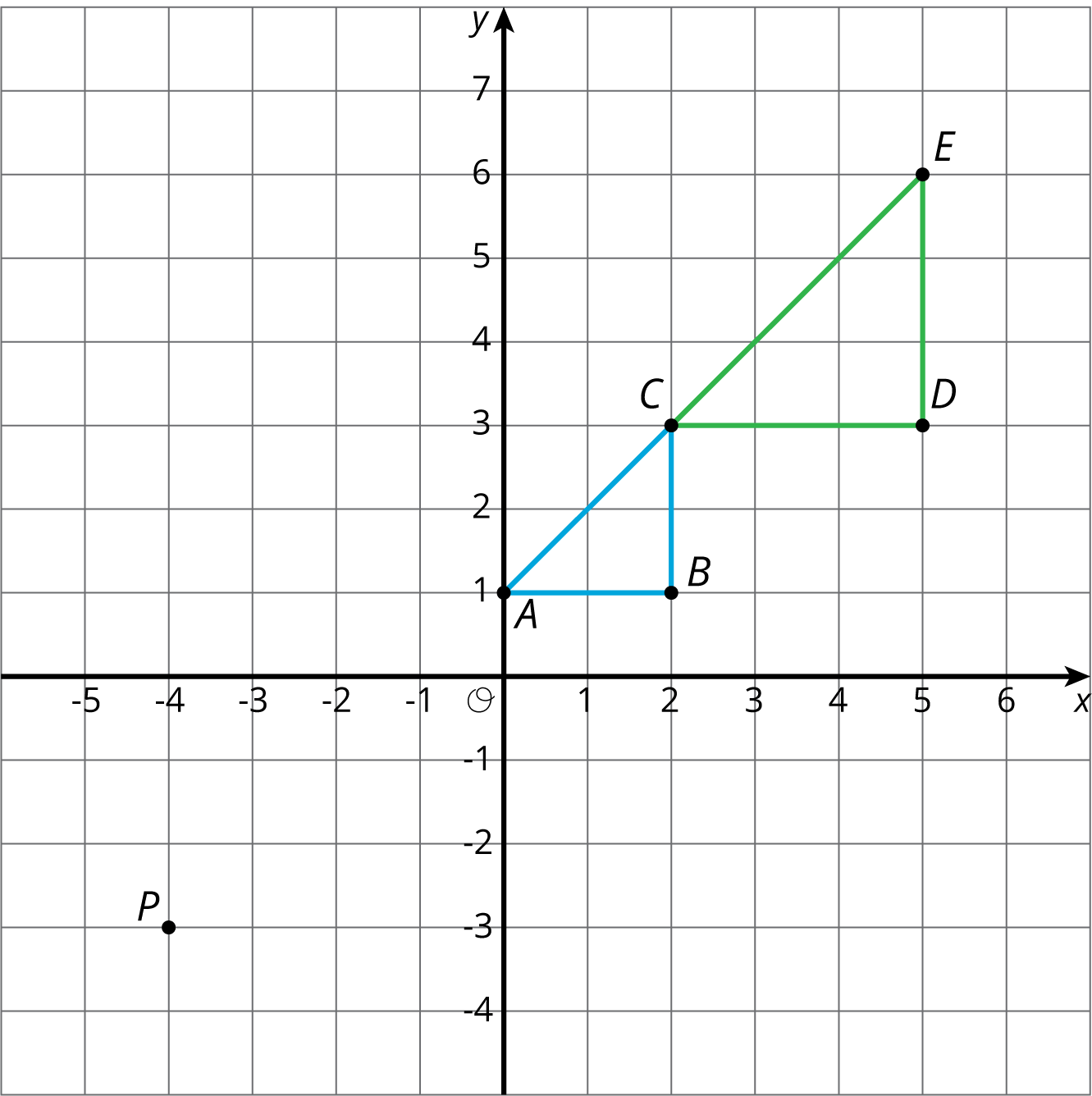
- D. Answers vary. Sample response: the dilation of the triangle will be a triangle and it will be larger than △ABC since the scale factor is larger than 1. This suggests card D. The two are plotted together and △CDEis the dilation of △ABC with center P and scale factor 32.
"Are you ready for more?" Student ResponseOriginal has center (4,0) and radius 4. Image has center (6,0) and radius 6.Activity SynthesisShare the correct answers and invite selected students to share the strategies they used to solve the problems. This is a matching problem, so students may not have dilated the entire image to find the correct answer among the choices. Important points to bring out include:- A dilation maps a circle to a circle, a quadrilateral to a quadrilateral, and a triangle to a triangle.
- If the center of dilation for a polygon is one of the vertices, then that vertex is on the dilated polygon.
- If the scale factor is less than 1 then the dilated image is smaller than the original figure.
- If the scale factor is larger than 1 then the dilated image is larger than the original figure.
- “How do we perform dilations on a square grid?”
- “How do coordinates help describe and perform dilations?”
The image of Q will be half as many grid lines to the left and half has many grid lines up—that is, 2 grid lines to the left and 1 grid line up from P.When the grid has coordinates, it is easier to communicate the location of new points. In the figure, we have A=(0,0) and B=(2,1).What is the dilation of B with center A and scale factor 3? To communicate the answer, we can just say (6,3). It is three times as far to the right and 3 times as far up from A as B so it is the desired point. COOL-DOWN: 5 minutes4.4: A Dilated ImageCCSS Standards: AddressingStudents apply a dilation to a polygon where the center of dilation is on the interior of the figure. The polygon is on a grid without coordinates and the structure of the grid can be efficiently used to find the dilation.Student-Facing Task StatementDraw the image of rectangle ABCD under dilation using center P and scale factor 12.Student ResponseLesson 3back to topLesson 5Community Created ResourcesCommunity-created resources were developed and submitted by educators using Open Up Resources 6–8 Math curriculum. Thank you to everyone who continues to contribute discussion, resources, and other materials to our community!Coming soon for this lesson.