E15 Egy alapelemű aperiodikus királis csempézés

Témák:2D vektorok (két dimenziós), Egybevágóság, Szerkesztések, Forgatás, Eltolás

Smith úr története

Vajon melyek azok a síkgeometriai alakzatok, amelyek egybevágó példányaival hézagmentesen, egy rétegben lefedhető a sík? Létezik-e véges sok olyan alakzat, amelyek alkalmasak az aperiodikus lefedésre, vagyis olyanra, amely eltolással nem vihető át önmagába? A kérdésnek komoly matematikatörténeti múltja és jelene van. Először egy 6 elemből álló erre alkalmas készlettel sikerült megoldani a problémát, majd 1974-ben Roger Penrose meg tudta oldani ugyanezt a kérdést egy mindössze két elemű készlettel. Azóta ebben a kérdésben nem történt jelentős előrelépés. Mígnem 2023. márciusában Smith úr, egy skót faluban élő nyugdíjas nyomdatechnikus, egy puzzle feladatokra kihegyezett programmal "játszva" fedezte fel, hogy egyetlen alapelem is elegendő a sík nem periodikus lefedéséhez. Ezt három, e témában jártas matematikus elemezte egy márciusban leadott dolgozatban. Bár az itt bemutatott nem periodikus lefedéshez egy elem is elegendő, de fel kell használni az elem tükörképét is. 2023. május végén ugyanezek a szerzők egy újabb dolgozatot nyújtottak be, amelyben az egyetlen elemnek csak ugyanazt a királis (azonos körüljárású) változatát használták a nem periodikus hézagmentes lefedéséhez, amit - nagyon szellemesen -"szellem"-nek neveztek el. Mi több: ezzel az elemmel kizárólag nem periodikusan fedhető le a sík. Ezzel periodikus csempézés nem állítható elő.

Spectre (=szellem, kísértet): az egy elemű aperiodikus királis kövezés - parkettázás - alapeleme

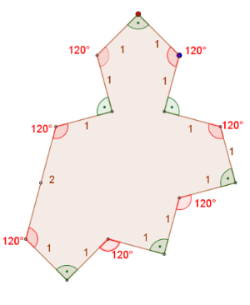
Addig amíg a márciusi - nem királis - lefedés alapelemeinek a csúcsai egy háromszögrács pontjaira illeszkedtek, az új változatnál ez már nem így van. A "szellem" olyan 14 oldalú sokszög, amelynek az oldalai egységnyiek, szögeik váltakozva ±90° és ±120°. Kivéve egyet, amely 180°-os. Így a vizsgált alakzat 13 oldalú sokszögnek is tekinthető.

Talán könnyebb dolgunk lenne az alapalakzat kézbe vehető példányaival lefednünk a sík egy darabját, most azonban arra teszünk kísérletet, hogy ezt a parkettázást a GeoGebra felhasználásával próbáljuk meg. Az alábbi appletben N és M dinamikusan mozgatható pont.

N a kezdő elem belső pontja, ezzel választhatjuk ki azt a csúcsot, amelyet a már felvett elemek szélén lévő M -el kiválasztott csúcspontba szeretnénk illeszteni.
Ha N a kezdő elem kiválasztott csúcspontjába, M a már lerakott alakzatok valamelyik csúcspontjába kerül, akkor jelenik meg a a lerakandó elem elfordítását vezérlő csúszka, és annak a lehetősége, hogy a kiválasztott helyre rögzítsük az így beállított elemet.
Az applet alkalmazása közben előfordulhat, hogy rossz helyre tettük le a "kézbe vett szellemet", ezért van lehetőség arra, hogy visszavonjuk az elhamarkodott rögzítést. Sőt az is előfordulhat, hogy jóval később derül ki, hogy a kövezés valahol nem folytatható, így több elemet is visszaszedhetünk.
Ha a szerkesztés kapcsolóval felfüggesztjük a munkát, meg tudjuk nézni, hogy e cikk szerzői milyen kövezést tekintettek folytathatónak. Ez persze nem jelenti azt, hogy csak ez az egyetlen járható út.

Figyeljük meg, hogy ...

... el tudunk-e lényegesen térni az említett cikkek alapján ajánlott elrendezéstől? Például próbáljunk elhelyezni az kezdő alapelem köré hat, (vagy több) "szellemet" úgy, hogy lehetséges legyen minden irányban a csempézés folytatása.
... az ajánlott elrendezést vizsgálva észrevehető, hogy a sötétebb színnel kiemelt "szellem" -hez minden esetben ugyanúgy csatlakozik egy, amellyel együtt egy tengelyesen szimmetrikus alakzatot alkot. Nevezzük ezt a kettőst - házi használatra - "Buddhának", mivel e két "szellem" közös kontúrja a Buddha szobrokra emlékeztet.
... az említett kiemelt elemek - durván - szabályos háromszögrácsot alkotnak. Az, hogy milyen irányban állnak egymáshoz viszonyítva Buddha formáját szemlélve jobban nyomon követhető.

[i]Buddha:[/i] két "szellem"-ből álló
tengelyesen szimmetrikus alakzat. — *Buddha:* két "szellem"-ből álló tengelyesen szimmetrikus alakzat.

Klaszterek

A fenti "felhasznált irodalom" ábráin azt láthattuk, hogy a már lerakott alapelemeket -szellemeket- többnyire 9 elemű csoportokra - a cikk szóhasználatát követve klaszterekre - osztotta. Minden klaszterben azonos a szellemek elrendezése. Ez ad lehetőséget arra, hogy egy ezeket a klasztereket egymáshoz illesztve lényegében kilencesével folytathassuk a sík lefedését. Az alábbi appletben fixen rögzítettünk kilenc szellemet, ezt tekinthetjük első klaszternek. A fenti applet eljárását erre alkalmazva az NM vektor és α megfelelő megválasztását követve rögzíthetünk- - vagy szükség esetén törölhetünk - egy egy új klasztert. A klaszterek kontúrjai elég cikk-cakkosak ahhoz, hogy segítség nélkül megfelelően egymáshoz illesszük őket. A "szerzői" megoldás láthatósága sokat segíthet a megoldás megtalálásában. Az alábbi applet bal felső sarkában van egy három állapotú kapcsoló, ezzel szabályozható, hogy a szellemek, vagy klasztereik összeillesztésével, vagy csak kapcsolataik elemzésével foglalkozzunk-e. Az alábbi applet alkalmazóira bízzuk annak a felderítését, hogy e szöveg elején miért van szükség a többnyire szó használatra. Van-e olyan klaszter, amelyet nem 9 szellem alkot?

Felhívjuk a GeoGebra fájlok táblázatainak a használatában jártas olvasóink figyelmét, hogy ezt a programot letöltve és offline üzemmódban használva, megnyílik a lehetőségük arra, hogy

az ideiglenesen félbehagyott parkettázást máskor folytassák;
a lerakott elemeket tetszőlegesen színezzék;
bővítsék az itt 100 szellem és 30 klaszter lerakására maximált programot;
elemezzék a lerakott alakzatok -és kaszterek - közötti matematikai kapcsolatokat,
másutt is alkalmazzák e programban használt technikai fogásokat.

Megjegyzés

Az, hogy "kitapogatjuk" a kézbe vett alapelem, vagy kalszter legcélszerűbb elhelyezését, messze nem elegendő ahhoz, hogy ezzel igazoljuk: az alapelemekkel valóban kikövezhető a sík, és ezt csak aperiodikus módon tehetjük meg. Ehhez - minden bizonnyal - olyan algoritmust kellene megadnunk, amellyel egyre nagyobb és nagyobb klasztereket lehetne előállítanunk, amelyek alkalmasak egy ilyen kövezésre.

Egy duplán lefedett szellem

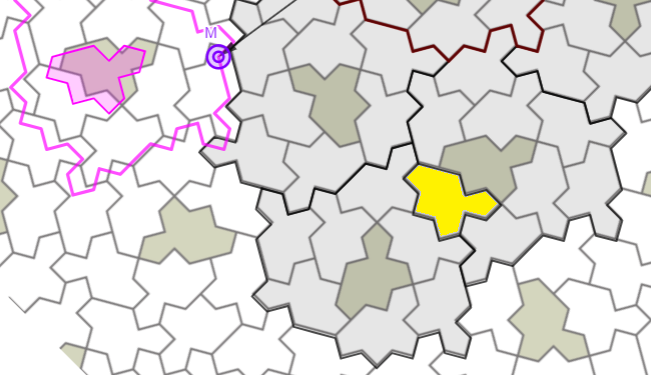
Előfordulhat, hogy az egymással egybevágó klaszterekkel történő lefedés csak úgy folytatható, ha egy-egy alapelem (szellem) két klaszter metszete, így ezt duplán is lefedtük. Ez lényegében nem baj, magának a problémának a megoldhatóságát nem befolyásolja. Azt mondhatjuk, hogy vannak 9 és 8 alapelemű klasztereink, és ezekből "kell" kialakítanunk egy nagyobb klasztert, aminek ugyancsak lehet a fenti értelemben vett hiányos változata. És így tovább. ... Nos, e sorok írója ezt a - lényegében a teljes indukció alkalmazásából ismert "... és így tovább ..." lépést egyelőre nem látja. Bár... lehet, hogy van ilyen. A kételkedés joga - és kötelessége azonban bizonyára ott van mindannyiunk gondolataiban.