Pontok, távolságok II. (9.)
Kattintgass a "T" gombra!
Láthatjuk, hogy a távolságok négyzetösszege akkor minimális, ha P az ABC háromszög súlypontja.
Felhasználtuk, hogy a vektor skaláris négyzete egyenlő a hosszának a négyzetével, azt, hogy a háromszög súlypontjából a csúcsaiba mutató vektorok összege nullvektor, és azt, hogy a nullvektor bármely vektorral képzett skaláris szorzata nulla.
c.)
A szorzat akkor 0, ha valamelyik tényező 0, így minimum akkor van. ha P=A vagy P=B vagy P=C. Maximum nincs.
A távolságok szorzata
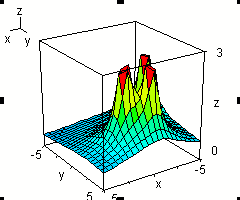
A fenti applet alapján sejthető, hogy ha a P az ABC háromszög belső pontja, akkor a vizsgált távolságszorzatnak maximuma van. Hol és mennyi?
Kísérletezzünk!
d.)
Kísérletezzünk!
7. probléma
Az ABC háromszög mely belső pontjára igaz, hogy az oldalegyenesektől való távolságainak
a) összege;
b) négyzetösszege
;c) szorzata;
d) reciprok összege
minimális illetve maximális?
a.) Kísérletezzünk
b.) Kísérletezzünk!
c.) Kísérletezzünk!
d.) Kísérletezzünk!
Ha a kísérletezés alapján sejtések, esetleg tételek születnének,akkor érdemes lenne azokat közreadni,