L5.6 - Scaling Solids
Learning Intentions and Success Criteria
- Comprehend that when a solid is dilated by a scale factor of k, its surface area is multiplied by k2 and its volume is multiplied by k3.
- Know that when a solid is dilated by a scale factor of k, its surface area is multiplied by k2 and its volume is multiplied by k3.
6.1: Math Talk: Cube Volumes
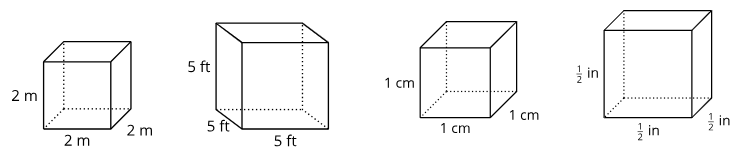
6.2: How Do Surface Area and Volume Change with Scaling?

2.
3. Suppose a unit cube is dilated by some scale factor k. a. Write an expression for the surface area of the dilated cube.
b. Write an expression for the volume of the dilated cube.
c. Compare and contrast the expression for surface area and the expression for volume.
6.3: Scaling All Solids
Clare says, “We know that if we dilate a cube by a factor of k, the cube’s volume is multiplied by k3. It seems like that must apply to all solids, but I’m not sure how to prove it.” Elena says, “Earlier in the unit, we showed that we can cover any two-dimensional shape with rectangles, so the property that area changes by k2 when we dilate a figure by k applies to all shapes, not just rectangles. Can we do something similar here?” 1. Use Elena’s line of reasoning to argue that for any solid, if it’s dilated by a factor of k, the volume is multiplied by k3.
2. Suppose a triangular prism has surface area 84 square centimeters and volume 36 cubic centimeters. The prism is dilated by scale factor k = 4. Calculate the surface area and volume of the dilated prism.


Learning Intentions and Success Criteria
- Comprehend that when a solid is dilated by a scale factor of k, its surface area is multiplied by k2 and its volume is multiplied by k3.
- Know that when a solid is dilated by a scale factor of k, its surface area is multiplied by k2 and its volume is multiplied by k3.
