Domínio das Variáveis
As variáveis que ocorrem em problemas representam quantidades que em geral só podem variar em uma certa faixa de valores possíveis, a qual chamamos de domínio da variável. Por exemplo, quando usamos a variável para nos referir ao volume do tanque no problema das duas torneiras, consideramos que assumia valores reais e maiores que zero, ou seja,
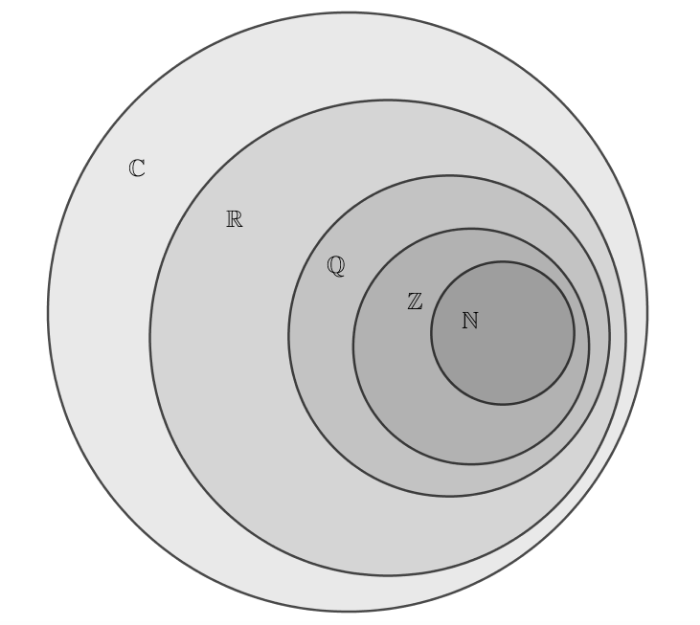
onde estamos usando a linguagem da Teoria dos Conjuntos para expressar o domínio de simbolicamente. Vamos relembrar os conjuntos numéricos mais importantes.Números Naturais
São os números usados para contar.
- Símbolo:
- Conjunto:
Números Inteiros
Os números inteiros estendem o conjunto de números naturais com números negativos para permitir
expressar a ideia de "falta" ou de "débito".
- Símbolo:
- Conjunto:
Números Racionais
Os números racionais estendem o conjunto de números inteiros com frações para permitir
expressar a relação entre parte e todo.
- Símbolo:
- Conjunto:
Números Reais
Os antigos matemáticos gregos descobriram que o comprimento da diagonal de um quadrado de lado um não pode ser expresso como uma fração ou razão entre dois números inteiros, ou seja, eles descobriram que existem números irracionais. O conjunto dos números reais estende o conjunto dos números racionais para incluir os números irracionais.
Se não indicarmos o domínio de uma variável, assumimos implicitamente que essa variável é real.
- Símbolo:
- Conjunto: É mais fácil pensar no conjunto geometricamente como o conjunto dos pontos de uma reta infinita.
Se não indicarmos o domínio de uma variável, assumimos implicitamente que essa variável é real.Intervalos
Na prática, a maioria das variáveis que ocorrem em problemas assumem valores reais e dentro de uma certa faixa de valores. Portanto, é conveniente introduzir o conceito de intervalo da reta e uma notação adequada para representá-lo. Quando escrevemos que
queremos dizer que pode assumir valores reais entre e , incluindo os valores de e . Se quisermos excluir a extremidade , por exemplo, usamos um parêntesis ao invés de colchetes. Explore as diversas possibilidades na figura interativa abaixo.Exercícios sobre Intervalos
- Represente o conjunto usando a notação de intervalo.
- Represente o conjunto usando a notação de intervalo.
- Represente o conjunto usando a notação de intervalo.
Números Complexos
Finalmente, os matemáticos descobriram que se acrescentarmos aos números reais um número com a propriedade que , equações algébricas sempre possuem soluções, e assim chegamos ao conjunto dos números complexos.
- Símbolo:
- Conjunto:
Domínio de uma Função
É muito frequente encontrarmos variáveis e que se relacionam de tal modo que para cada valor de em um certo domínio podemos associar um único valor de . Nesse caso dizemos que é uma função de , com domínio . Por exemplo, se , claramente para todo podemos calcular um valor bem definido de . Vemos assim que o domínio dessa função é o conjunto .
É muito comum darmos um nome para a função, tal como , etc., de modo que podemos também dizer que tem domínio . A ideia aqui é que podemos pensar a função como uma máquina que calcula um valor para todo . Por exemplo, .
Exercícios sobre Domínio de uma Função
Determine o domínio das seguintes funções: