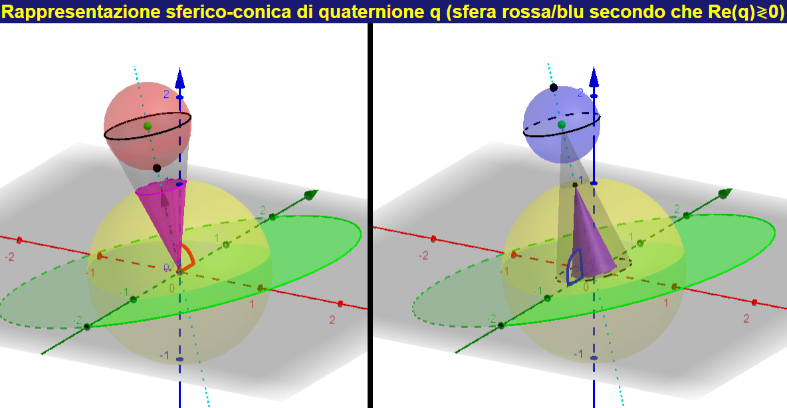
Rappresentazione sferico-conica dei quaternioni
I quaternioni sono vettori quadridimensionali dotati, oltre che della possibilità di essere addizionati, di quella di essere moltiplicati - a guisa dei numeri complessi - scrivendoli nella forma q=a+bi+cj+dk e utilizzando, oltre alle proprietà di corpo non commutativo, le relazioni: i² = j² = k² = ijk = -1. Due quaternioni unitari (ossia di modulo a²+b²+c²+d² pari a 1) opposti q e -q descrivono la stessa rotazione di un vettore tridimensionale v = x i + y j + z k mediante la formula v' = qvq* (dove q*=a-bi-cj-dk è il "coniugato" di q=a+bi+cj+dk). Per rotazione si intende quella antioraria, intorno ad un asse di versore u, di un angolo α. Quindi per ottenere le rotazioni spaziali basta la semisfera quadridimensionale unitaria dei quaternioni con a>0, rappresentabile con i punti interni alla sfera tridimensionale unitaria con l'identificazione: (b,c,d) <--> (√(1-b²-c²-d²),b,c,d)=a+bi+cj+dk (pensando a come potremmo rappresentare i punti di una superficie semisemisferica tramite i punti - anche interni - del suo cerchio base), arricchita con i quaternioni unitari avanti a=0 e d>0, rappresentabili (tramite la su data associazione) con la superficie semisferica unitaria tridimensionale superiore, con i quaternioni unitari tali che a=0, d=0 e b>0, rappresentabili col semiequatore unitario di suddetta sfera unitaria tridimensionale, e infine col quaternione unità (1,0,0,0), rappresentabile tridimensionalmente tramite (1,0,0). Queste parti di frontiera vengono "incollate" topologicamente ognuna alla rispettiva parte opposta, appunto identificando tra di loro quaternioni mutuamente opposti. Ogni quaternione q=a+bi+cj+dk è somma della sua parte reale a=Re(q) e della sua parte immaginaria bi+cj+dk=Im(q), la quale ha per modulo la lunghezza |Im(q)| di tale ultimo vettore. La forma polare di un quaternione p con parte immaginaria non nulla si ottiene nel seguente modo: - scrivendo p come multiplo, con fattore |p|, del quaternione unitario q=p/|p|; - scrivendo q come somma Re(q)+Im(q), con (Re(q))²+|Im(q)|²=1; - collocando il punto ( Re(q) , |Im(q)| ) sulla semicirconferenza goniometrica superiore; - determinando θ in ]0,π[ in modo che: cos θ = Re(q) e sin θ = |Im(q)|; - scrivendo q = cos θ + ( sin θ ) u, dove u = Im(q) / |Im(q)| è un versore tridimensionale, e ottenendo quindi la forma polare: p = |p| ( cos θ + ( sin θ ) u ) = |p| ( cos θ + ( sin θ ) Im(p) / |Im(p)| ). In tal modo i quaternioni unitari con parte reale positiva e parte immaginaria non nulla avranno θ in ]0,π/2[, mentre con θ=π/2 si otterranno quelli con parte reale nulla, quindi coincidenti con la loro parte immaginaria e rappresentati sulla superficie della semisfera tridimensionale unitaria superiore arricchita dei punti di frontiera precedentemente descritti. La rotazione di cui sopra ha proprio u come versore d'asse e l'angolo α di cui v ruota in senso antiorario, per produrre qvq*, è pari proprio al doppio di θ. http://tinyurl.com/ssuqr http://tinyurl.com/ssuqc Il prodotto fra due quaternioni Q = bi + cj + dk Q' = b'i + c'j + d'k, entrambi con parti reali nulle, è esprimibile mediante prodotto scalare ● e prodotto vettoriale Λ nel seguente modo: QQ' = -Q●Q' + QΛQ'. Infatti ciò vale per Q,Q'∈{i,j,k} e si estende mediante la bilinearità delle operazioni (Q,Q')→QQ' (Q,Q')→Q●Q' (Q,Q')→QΛQ'. Inoltre l'operatore Q→qQq* (con q quaternione fissato) è lineare; quindi: q(hQ+kQ')q* = h(qQq*)+k(qQ'q*). Pertanto: 1) se q è unitario e ha parte immaginaria nulla, allora q=±1, per cui qQq* = Q 2) se q è unitario e ha parte immaginaria non nulla, allora q ha forma polare e: q = cos θ + u sin θ q*= cos θ - u sin θ con u= Im(q)/|Im(q)|. In tal caso possiamo determinare qQq* scrivendo: Q=hv+ku, con v⊥u e |v|=1, ottenendo: q(hv+ku)q* = h(qvq*)+k(quq*). Ma: qvq*=(cosθ+u sinθ)(v cosθ-v u sinθ) = (cosθ+u sinθ)(v cosθ+v●u sinθ-vΛu sinθ) = (cosθ+u sinθ)(v cosθ-vΛu sinθ) = v cos²θ+uv sinθcosθ-vΛu sinθcosθ-u(vΛu)sin²θ = v cos²θ+(-u●v+uΛv)sinθcosθ-vΛu sinθcosθ-(-u●(vΛu)+uΛ(vΛu))sin²θ = v cos²θ+(uΛv)sinθcosθ-vΛu sinθcosθ-(uΛ(vΛu))sin²θ = v cos²θ+(uΛv)sinθcosθ-vΛu sinθcosθ-v sin²θ = v(cos²θ-sin²θ )+(uΛv)sinθcosθ-vΛu sinθcosθ = v cos 2θ + uΛv sin 2θ e: quq*=(cos θ+u sin θ)(u cos θ-uu sin θ) = (cosθ+u sinθ)(u cosθ+u●u sinθ-uΛu sinθ) = (cosθ+u sinθ)(u cosθ+sinθ) = u cos²θ+uu sinθcosθ+sinθcosθ+u sin²θ = u+(-u●u+uΛu)sinθcosθ+sinθcosθ = u+(-1+0)sinθcosθ+sinθcosθ = u, per cui: q(hv+ku)q*=h(v cos2θ + uΛv sin2θ)+ku, ossia il ruotato di v dell'angolo 2θ intorno a u in senso antiorario. Si possono rappresentare i quaternioni unitari aventi parte reale negativa (e per estensione quelli non unitari, modificati dagli unitari con omotetia di fattore pari al loro modulo) con coni di apotema unitaria aventi il centro della base nell'origine. Per contro i quaternioni unitari con parte reale positiva sono rappresentati da coni di apotema unitaria aventi il vertice nell'origine (e anche per essi la moltiplicazione per un fattore di omotetia positivo fornisce il quaternione avente per versore il quaternione unitario dato e per modulo tale fattore). Pertanto il modulo di un quaternione è l'apotema del suo cono rappresentativo. I quaternioni unitari con parte reale nulla diventano segmenti di lunghezza unitaria con un estremo nell'origine, in cui degenerano (l'apotema viene a coincidere con l'altezza) entrambi i suddetti coni quando l'angolo della rappresentazione polare (l'argomento del quaternione) diventa π/2. Visti come punti o vettori della sfera unitaria nello spazio tridimensionale, essi generalizzano allo spazio il concetto di unità immaginaria del campo complesso. Quando, invece, la parte immaginaria diventa nulla i coni degenerano nella loro base, che è un cerchio centrato nell'origine. Considerando quanto suggeriscono le rotazioni illustrate in http://tinyurl.com/ssuqc http://tinyurl.com/suqprnp1 (che in tal caso diventano di 0 e 2π), possiamo distinguere tra cerchi vuoti (circonferenze) centrati nell'origine - associate all'argomento 0 e ai numeri reali positivi - e cerchi pieni centrati nell'origine - associati all'argomento π e ai numeri reali negativi. Il che significa che i coni con vertice nell'origine degenerano nel raggio di base e gli altri nell'opposto del raggio di base. http://tinyurl.com/sferuniquat Possiamo formalizzare e compendiare tutto questo utilizzando i concetti di sfera chiusa: S⁺(P,r)={P' : |P-P'|≤r} e sfera aperta: S⁻(P,r)={P' : |P-P'|<r}. Ogni sfera S⁺(P,0)={P} è identificabile con P (quaternione immaginario puro, alias punto 3d). In particolare S⁺(O,0) rappresenta il quaternione nullo. Ogni sfera chiusa non vuota S⁺(P,r) con r>0 e P≠O è associata al cono C⁺(P,r) con vertice nell'origine O e base: B(P,r) := S⁺(P,r) ∩ piano_perpendicolare(OP,P) e rappresenta il quaternione di parte reale r e di parte immaginaria P; il suo modulo è la distanza tra O e la circonferenza bordo di tale base, ossia l'apotema del suddetto cono; il suo argomento è in ]0,π/2[. Ogni sfera chiusa S⁺(O,r) con r>0, corrispondente alla degenerazione del cono C⁺(P,r) per P=O, rappresenta il quaternione di parte immaginaria nulla e parte reale r. La rappresentazione polare di tale quaternione non è definita, ma si può assumere come argomento il valore zero (come per i numeri reali positivi nel piano complesso). In particolare S⁺(O,1) rappresenta il quaternione unità. Ogni sfera aperta non vuota S⁻(P,r) con r>0 e P≠O è associata al cono C⁻(P,r) con vertice nel punto P e base: B(P,-r) := S⁺(O,r) ∩ piano_perpendicolare(OP,O) e rappresenta il quaternione di parte reale -r e di parte immaginaria P; il suo modulo è la distanza tra P e la circonferenza bordo di tale base, ossia l'apotema del suddetto cono; il suo argomento è in ]π/2,π[. Ogni sfera aperta non vuota S⁻(O,r) con r>0, corrispondente alla degenerazione del cono C⁻(P,r) per P=O, rappresenta il quaternione di parte immaginaria nulla e parte reale -r. La rappresentazione polare di tale quaternione non è definita, ma si può assumere come argomento il valore π (come per i numeri reali negativi nel piano complesso). Possiamo, in alternativa, sostituire alle sfere chiuse le loro frontiere ∂S(P,r) (superfici sferiche), con l'unica differenza che le basi dei coni si riducono da cerchi a circonferenze. In tal caso la polarizzazione si esprime in sfere vuote e sfere piene. Un'altro modo di gestire la differenziazione sferica può essere quello di sfruttare l'orientabilità delle superfici sferiche (ovvero la distinzione tra due facce, una esterna e una interna), considerandole orientate verso l'esterno (positive) o verso l'interno (negative). http://tinyurl.com/sferuniquat1 http://tinyurl.com/sferuniquat2 http://tinyurl.com/sferuniquat3 http://tinyurl.com/sferuniquat4 In particolare, i quaternioni unitari con parte immaginaria non nulla possono essere rappresentati - se la parte reale è non negativa - dai paralleli sulla sfera unitaria dell'ordinario spazio tridimensionale (ossia le circonferenze giacenti su di essa e aventi assi passanti per l'origine) e dai loro cerchi (o dalle calotte minori) - se la parte reale è negativa. Inoltre, le curve quaternioniche (se sufficientemente "regolari") sono rappresentabili da tubi 3d - vuoti o pieni a tratti - la cui "anima" è la curva costituita dalle parti immaginarie e le cui sezioni normali ad essa sono circonferenze o cerchi i cui raggi sono il valore assoluto delle parti reali, il cui segno è negativo nel caso si tratti di cerchi e non circonferenze.