Test jezelf

Vraag 1

Er is verband tussen de grafiek en de hellingsgrafiek van een functie. a. Wat betekent het voor de grafiek van de functie als de hellingsgrafiek onder de x -as ligt?

De functiewaarden zijn dan negatief.
De grafiek is dan afnemend dalend.
De grafiek is dan dalend.

De grafiek heeft dan een minimum.

b. Soms is een grafiek toenemend stijgend. Hoe zie je dat aan de hellingsgrafiek?

De hellingsgrafiek is stijgend.
De hellingsgrafiek ligt boven de x -as en is stijgend.
De hellingsgrafiek heeft een maximum.

c. Hoe vind je de x -coördinaten van de toppen van de grafiek van een functie uit de hellingsgrafiek?

Je bekijkt voor welke waarden van x de hellingsgrafiek een maximum of een minimum heeft.
Je bekijkt voor welke waarden van x de helling de waarde 0 heeft.
Die kun je niet uit de hellingsgrafiek alleen aflezen.

d. Hoe vind je de nulpunten van de grafiek van een functie in de hellingsgrafiek?

Die kun je niet uit de hellingsgrafiek alleen aflezen.
Daar waar de hellingsgrafiek de x -as snijdt.
Bij de toppen.
Daar waar de hellingsgrafiek van toenemend stijgend (of dalend) overgaat naar afnemend stijgend (of dalend) of omgekeerd.

Vraag 2

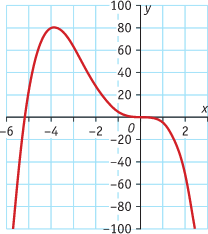
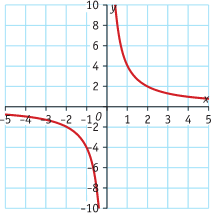
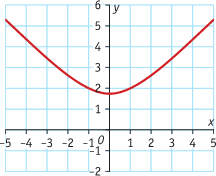
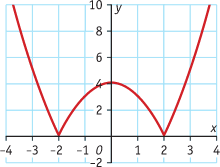
Bekijk de grafieken. a. Schets bij elk van de grafieken de hellingsgrafiek. b. Grafiek B heeft een verticale asymptoot. Wat betekent dit voor de hellingsgrafiek? c. Wat is er aan de hand met de hellingsgetallen van de raaklijnen bij punten die op de x -as liggen bij grafiek D?

A

B

C

D

Vraag 3

Bekijk het tekenschema van de hellingsfunctie van een functie g. Schets een mogelijke grafiek van g.

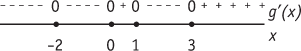
Vraag 4

Bekijk de hellingsgrafiek van functie f.

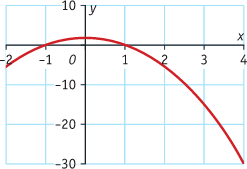
a. Op welk interval stijgt de grafiek van f? b. Voor welke waarden van x heeft de grafiek van f een maximum? c. Kun je uit de hellingsgrafiek aflezen hoe groot dit maximum is? d. Neem aan dat f(0) = 2. Teken nu de grafiek van f.

Vraag 5

Een auto trekt op als het stoplicht op groen springt. Voor de afgelegde weg geldt: s(t) = 1,6t² , waarin s de afgelegde weg in meter is en t de tijd in seconden. a. De snelheid van deze auto wordt uitgedrukt in meters per seconde. Teken de grafiek van de snelheid v van deze auto als functie van de tijd t. Maak eerst een tabel. b. Stel een bijpassende formule op voor de snelheid v(t) gebaseerd op de gevonden gegevens. c. Na hoeveel seconden is de snelheid meer dan 80 km/h? Geef je antwoord in één decimaal nauwkeurig.

Vraag 6

Gegeven is de functie f(x) = 2x²+ 5x + 3. Stel de formule op van de hellingsgrafiek van f door eerst een tabel te maken.

Vraag 7

Je ziet een hellingsgrafiek van een functie g. Schets een mogelijke grafiek van g.

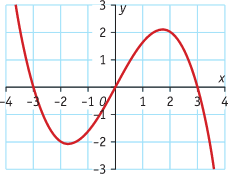
Vraag 8

Er zijn vier functies gegeven:

a. Bereken voor elk van deze functies het hellingsgetal van de raaklijn voor x = 1. b. Teken van elk van deze functies de grafiek van de hellingsfunctie. c. Bepaal met behulp van de hellingsgrafiek de extremen van de gekozen functie.

Vraag 9

Gegeven is de functie f(x) = -0,5x²+ 4x. a. Stel een formule op voor de hellingsfunctie f'(x) door eerst een tabel van f' te maken. b. Laat zien hoe je deze formule kunt afleiden door het differentiequotiënt op [x, x+h] te herleiden. c. Beredeneer wat de formule van de hellingsfunctie g' met g(x) = -0,5(x−4)² zal zijn zonder gebruik te maken van een tabel of een differentiequotiënt.