Contenu
Números complejos. Matemáticas Bachillerato
Números complejos
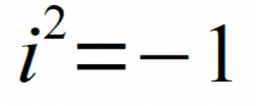
Table des matières
1. ¿Por qué definir números complejos?
2. Unidad imaginaria y notación binómica
3. Suma, resta y producto en notación binómica
4. Conjugado y división en notación binómica
5. Raíz cuadrada en notación binómica
6. Potencia de la unidad imaginaria
7. Potencia en notación binómica y binomio de Newton
8. Notación afija y plano complejo
9. Módulo y fase en notación polar
10. Notación trigonométrica
11. Producto y cociente en notación polar
12. Potencia en forma polar
- Teoría - 12 - potencia en forma polar
- Problemas resueltos - 12 - potencia en forma polar
- Taller Geogebra: potencia en complejo de módulo inferior a la unidad
- Taller Geogebra: polígono formado por potencias de complejos de modulo igual o inferior a la unidad
- Taller Geogebra: polígono y potencia en complejos de módulo superior a la unidad
- Geogebra actividad - Geometría con números complejos
- Geogebra actividad: solución a geometría con potencias de números complejos
- 1 BCT Representación de las potencias de números complejos
- Potencias de complejo de módulo 1
13. Raíces en forma polar
14. Distancia entre puntos del plano complejo
15. Fórmula de Moivre
16. Ecuación de Euler para números complejos
17. Teorema fundamental del álgebra