5.ベクトルと内積
このページは電子ブック「探求 数学B・C」の一部です。
★折れ線の最短矢印がベクトル
1.ベクトルは最短矢印
<ベクトルの連結と最短化>
ベクトル[Vector]は移動の始点[Starting poit]と終点[Ending point]を結ぶ矢印[Arrows]です。
途中点は省けます。
・つまり、ベクトルの和は折れ線の進行の最短矢印
ベクトルの終点AにベクトルABの始点Aをつなぐと折れ線[polyline]になっても始点がOで終点がBです。
最短矢印はベクトルOBになる。始点を原点に束縛した[binding]ベクトルは終点がベクトルの位置を示すので位置[position]ベクトルといいます。一方で、始点を原点にかぎらないベクトルは自由[freedom]ベクトルで、平行移動して動かせます。
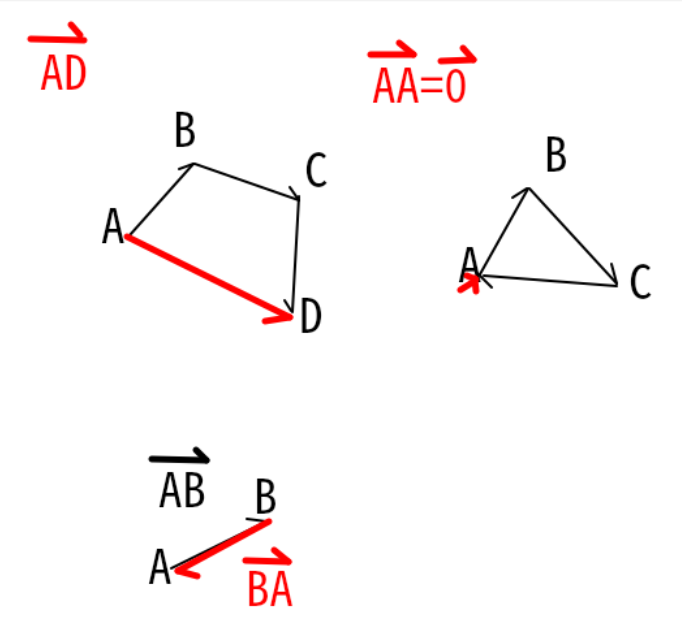
・では、A→B→C→Dと折れ線で移動したとしましょう。
これはAが始点で終点がDの移動矢印なので、ベクトルADで、 と書きます。
矢線が表示できない環境では、太字にしたり、2重字にしたりして、スカラー量(1軸に詰め込める実数)とは区別する。
途中点を省略しないと と3つの矢印をつないだものとも言えます。
だから、 となります。
・A→B→C→Aの折れ線移動はどうでしょうか?
最終的に になる。ベクトルAAは結果的に移動の道のりはゼロではないが、
距離としてはゼロなのでゼロ[zero]ベクトルです。大きさも向きもありません。
・A→B→AのUターンはどうでしょうか?
ベクトルABとベクトルBAは向きが逆で大きさが同じなので、逆[reverse]ベクトルといいます。
<ベクトルの演算>
・ベクトルの定数k倍[Constant times]
移動量が1のベクトルを単位ベクトルといいます。
また、ベクトルに定数kをかけたベクトルを定数倍のベクトルといいます。
定数k倍のベクトルは長さが|k|倍になり、向きがkが負のときに反転します。
・ベクトル和=対角線[diagonal]で、交換可能[replaceable]
・ベクトルの和
和ベクトルは2ベクトルが作る平行四辺形[parallelogram]の対角線ベクトル。
となるように、ベクトルOBを平行移動して、Aにつなぐと、折れ線O→A→Cの移動、
つまり、ベクトルOCになります。これは2ベクトルOB,OAを2辺とする平行四辺形の対角線ベクトル
になります。
和の順番を逆にすると、折れ線O→B→CでもベクトルOCができるはずです。
ベクトル和は交換可能です。
・ベクトルの差
差ベクトルは引く点位置から引かれる点位置への移動ベクトル。
逆ベクトルとの和ベクトルを求めると考えると、交換可能になる。
だから、B→O→Aの折れ線移動だから、ベクトルBAと等しい。
・ベクトルの差の使い道は「ベクトル始終=O終ーO始」
ベクトル差の考えは、図形の頂点を結ぶベクトルを位置ベクトルに直すときによく使います。
例えば、三角形ABCの問題などでは、ベクトルABとACの内積やそれぞれの絶対値を求めたりします。
このとき、ベクトルAB=b-a,ベクトルAC=c-aなどのように位置ベクトルで表すことで、図形の問題を
位置ベクトルの絶対値や内積の問題に直しやすくなったりします。
2.ベクトルの分解と成分
<ベクトルの合成と分解>
ベクトルaと平行でないベクトルbがあるとき、定数sと定数tを使い、ベクトルcが
と合成[composition,synthesis]できる。
ベクトルcがゼロになるのは、s=t=0のときに限定される。これをaとbの1次独立という。
逆に、ベクトルcを2つのベクトルa,bを使って
と分解[decomposition,disassembly,analysis,breakdown]できる。
そのときのs,tはベクトルa成分[component,element]、b成分といい、 とかける。
(例)
「3点の座標をA(3,0,0),B(2,1,2),C(1,-2,2)とするとき三角形ABCの面積」は?
ベクトルAB=(-1,1,2)、AC=(-2,-2,2)となるから、それぞれの絶対値の2乗と内積の2乗は、
1+1+4=6, 4+4+4=12, (2-2+4)2=16だから、面積は1/2√(6・12-16)=√14。
<基本ベクトルと成分>
x軸の正方向の単位ベクトル、y軸の正方向の単位ベクトルをそれぞれ とすると、
座標が(s,t)の点Aがあるとき、ベクトルOA= と分解でき、s,tがx成分、y成分となる。
このとき、ベクトルOAの大きさは となる。
(例)斜交座標
「 とし,s,t,s+tの絶対値が1以下とする。ベクトルcの存在範囲」は?
点(x,y)=(s,t)の存在範囲はy=-x+1以下でy=-x-1以上で、xが-1以上1以下、yが−1以上1以下の領域になる。この図形の基本ベクトルはx軸、y軸の単位ベクトルにしたときに、成分が(s,t)になっている。
そのかわりにベクトルa,ベクトルbを基本ベクトルにしたときの成分が(s,t)になるように、座標変換した領域をかけばよい。
・ベクトルの相等、和・差・定数倍は各成分の相等、和・差・定数倍に落とし込める。
ベクトルa=(ax, ay), b=(bx,by)とするとき、
aとbが平行であることは、成分の上でどうなるでしょうか。
平行ということはa=kbとなるゼロでない定数kがあるということです。
成分でみると、ax=kbx ,ay=kbyです。kについて解くとk=ax/bx=ay/byとなります。
だから、axby-aybx=0と成分のたすきがけの差がゼロということです。
a//b=axby-aybx
内積は符号つきの2線分の積だね。
3.ベクトルの内積
<内積の定義>
2つのベクトルa,bがあるとき、内積a・b(ドット積)[inner product, dot product,scalar product]とはベクトルの作る角をθとすると、
で、
cosθの絶対値が1以下だから、
内積a・bの絶対値は|a||b|以下になります。
1つのベクトルを他方に正射影した有向サイズと他方のベクトルのサイズをかけたもの。
有向サイズとサイズの積なのでベクトルではなく、スカラー量です。
*geogebraでは、dot(a,b)と入力するとベクトルa,bの内積を返します。
cosθを使う射影ベクトルのサイズが最大になるのはθ=0、または、θ=πのとき。
・同じ向きで2ベクトル重なる(θ=0)なら、2ベクトルの類似度は最大になり、
内積a・b=2ベクトルの大きさの積=|a||b|
・反対向きで2ベクトルが同一直線上(θ=π)なら、2ベクトルの類似度は正反対で最大になり、
内積a・b=ー2ベクトルの大きさの積=-|a||b|
・cosθを使う射影ベクトルのサイズが最小0になるのはθがπ/2, 3/2 πのときだから、
2ベクトルが垂直と内積a・b= 0は同値。
内積もサイズも計算されたとすると、内積の定義から2ベクトルのコサインがわかります。
。
<内積の成分>
(2次元ベクトル)a=(ax, ay), b=(bx,by)ならば、a・b=axbx+ayby
(理由)
余弦定理とピタゴラスを使い数式比較するだけです。
2ベクトルの差a-b=cとする。
ベクトルの絶対値をそれぞれAa,Ab,Acとする。
Aa2=ax2+ay2, Ab2=bx2+by2、Ac2=(ax-bx)2+(ay-by)2=Aa2+Ab2-2(axbx+ayby)
一方で、余弦定理から、Ac2=Aa2+Ab2-2(AaAbcosθ)
2式のカッコの中も一致するから、a・b=Aa・Ab・cosθ=ax・bx+ay・by
(3次元ベクトル)a=(ax, ay, az), b=(bx,by,bz)ならば、a・b=axbx+ayby+azbz
<内積の計算法則>
内積は定義上ベクトルの2つの長さの積とcosθの積だから、交換可能です。a・b=b・a
また、定数倍はくくりだすことができます。内積は和差と分配法則が成り立つので
a・(b+c)=a・b+a・cが成り立つことで、ベクトルの式を単純化できます。
また、a・a=|a|2となることも、数式の単純化に使います。
注意すべきなのは、逆に|a|2がa2ではなく、a・aと内積にすることです。
(例)
「位置ベクトルa,b,cについて、内積がa・a=8,b・b=4,a・b=3,b・c=2,c・a=4のとき、
cをa,bの一次結合で表す」には?
c=xa+ybとおく。両辺にaをかけて、a・c=xa・a+ya・b。内積値から4=8x+3y。
両辺にbをかけた場合は、b・c=xb・a+yb・b。内積値から2=3x+4y。
連立して解くとx=10/23、y=4/23。