Angle-Angle-Side (Or SAA)
AAS Illustrated
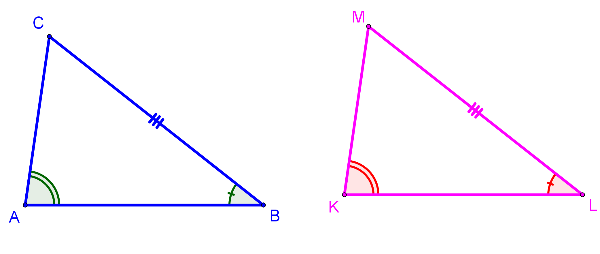
AAS Explained
If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
This is an extension of ASA. In ASA, since you know two sets of angles are congruent, you automatically know the third sets are also congruent since the sum of the interior angles are 180º in each triangle.
The "non-included" side in AAS can be either of the two sides that are not directly between the two angles being used.
Below is an example how to construct this. If you change anything in the construction, just click on the arrows on the top right to restore the construction.
Example: Constructing AAS
Steps in constructing AAS
Now you try to draw a triangle congruent to the previous one You need to draw a triangle with side AB=8cm an angle CAB of 40 degrees and angle BCA of 110 degrees. Try to do this in the "Applet" below
- Use
 to draw segment AB and if you are requested to give the length type in 5
to draw segment AB and if you are requested to give the length type in 5 - Use
 to draw an angle at point A. (Hint: Always click last on the point where you want the angle.) If requested for the angle size type in 40 degrees. Lastly you need to select clockwise or counterclockwise. The direction of movement is from the line in a clockwise or counterclockwise direction.
to draw an angle at point A. (Hint: Always click last on the point where you want the angle.) If requested for the angle size type in 40 degrees. Lastly you need to select clockwise or counterclockwise. The direction of movement is from the line in a clockwise or counterclockwise direction. - Use
 to draw a ray from point A through point B' that were created by the angle tool.
to draw a ray from point A through point B' that were created by the angle tool. - The problem is you cannot draw the next angle as you do not know the length of side AC. But you do know that the sum of the interior angles of a triangle is 180 degrees. This imply that angle ABC=180-(40+110). Now I can construct an angle at point B.
- Use
 to draw an angle at point B. If requested for the angle size type in 30 degrees.
to draw an angle at point B. If requested for the angle size type in 30 degrees. - Use
 to draw a ray from point B through point A' that were created by the angle tool.
to draw a ray from point B through point A' that were created by the angle tool. - Use
 to place point C at the intersection of the two rays
to place point C at the intersection of the two rays
- Use
 to draw triangle ABC
to draw triangle ABC
Exploring AAS
This is the same as for ASA. (See previous lesson)