L'incentro
Cosa abbiamo visto
Teorema Le bisettrici degli angoli interni di un triangolo si incontrano in un punto
Definizione Il punto di incontro delle bisettrici degli angoli interni di un triangolo si chiama incentro.
Il nome è chiarito dalla parte finale della costruzione vista sopra.
Proprietà L'incentro è il centro della circonferenza inscritta al triangolo.
Corollario Ogni triangolo è circoscrivibile a una circonferenza.
Attività 1: Verifichiamo il teorema
Cosa faremo:
- costruiamo il triangolo
- individuiamo le bisettrici dell'angolo A e dell'angolo B (nascondiamo le bisettrici degli angoli esterni)
- individuiamo il punto di intersezione
- tracciamo la bisettrice del terzo angolo e verifichiamo
- Costruiamo un triangolo a nostro piacere
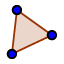
- Individuiamo le bisettrici
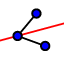di due vertici [nascondiamo le bisettrici degli angoli esterni: clicchiamo sull'oggetto con il tasto destro del mouse e dal menù "mostra oggetto"] - Individuiamo il punto di intersezione
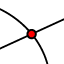e rinominiamo con I - Tracciamo la bisettrice dell'ultimo angolo e verifichiamo che il punto I appartiene a quest'ultima.
La dimostrazione del teorema
Ipotesi: ABC triangolo
Tesi: le bisettrici angoli interni si incontrano in un punto
Dimostrazione
a) Tracciamo le bisettrici degli angoli A e B del triangolo. Sia I il punto di intersezione
b) Mandiamo da I tre segmenti perpendicolari ai lati: ID, IE, IF
c) Ricoridamo la proprietà dei punti di una bisettrice: sono equidistanti dai lati dell'angolo
d) Pertanto per la proprietà: IF=IE e IF=ID e quindi IE=ID
e) Il punto I è dunque equidistante anche dai lati dell'angolo C, ovvero il punto I appartiene alla bisettrice dell'angolo interno C (per la proprietà in c)
CVDCostruiamo la dimostrazione con Geogebra
Continuiamo con il foglio precedente e
7) Tracciamo la retta passante per I e perpendicolare ad AB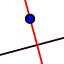 
8) Individuiamo il punto di intersezione tra la retta e il lato AB e rinominiamolo E
9) Nascondiamo la retta perpendicolare costruita e tracciamo il segmento IE 
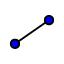10) Ripetiamo i punti 7,8,9 anche per gli altri due lati.
11) Per verificare che I è equidistante dai punti trovati sopra, possiamo costruire una circonferenza di centro I e passante per uno dei punti trovati (ad esempio E)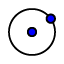 
La circonferenza trovata è quella inscritta nel triangolo.
8) Individuiamo il punto di intersezione tra la retta e il lato AB e rinominiamolo E
9) Nascondiamo la retta perpendicolare costruita e tracciamo il segmento IE
10) Ripetiamo i punti 7,8,9 anche per gli altri due lati.
11) Per verificare che I è equidistante dai punti trovati sopra, possiamo costruire una circonferenza di centro I e passante per uno dei punti trovati (ad esempio E)
La circonferenza trovata è quella inscritta nel triangolo.
Concludiamo e riassumiamo
Proprietà L'incentro è il centro della circonferenza inscritta al triangolo.
Dimostrazione
- si individui il punto I= incentro
- si tracci la circonferenza di centro I e raggio ID
- Poichè abbiamo dimostrato che i tre lati sono perpendicolari ai segmenti ID, IE, IF, possiamo affermare che i tre lati sono tangenti alla circonferenza (per la proprietà vista sulle tangenti ad una circonferenza)
- Pertanto la circonferenza tracciata è inscritta nel triangolo
CVD Corollario Ogni triangolo è circoscrivibile a una circonferenza.
Riassumendo:
- definizione di Incentro:
- Incentro è: centro della circonferenza …...
- Ogni triangolo è …... in una circonferenza
- Come trovare al circonferenza inscritta: … …