Doppler effect
Misschien kende je de naam niet, het effect ken je zeker.
Wanneer een wagen voorbijrijdt, daalt het geluid dat je hoort plots na het voorbijrijden.
Hoe groter de snelheid, hoe groter het geluidsverschil.
Dit effect is genoemd naar de Oostenrijker Christian Doppler die het midden de 19e eeuw beschreef.
Ook hier moeten we kijken naar wat er gebeurt met de geluidsgolven van een bewegende bron.
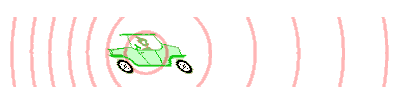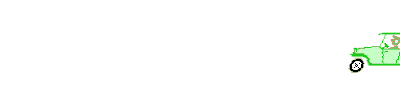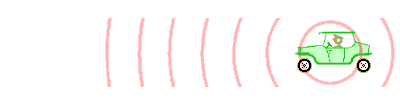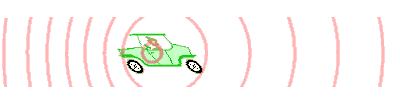Elke golf van de naderende auto doet er een welbepaalde tijd over om de waarnemer te bereiken.
De volgende golf moet een iets kleinere afstand afleggen, omdat de auto nu dichterbij is.
De waarnemer ontvangt de golven in een net iets hogere frequentie dan wanneer de auto stilstaat.
Dat komt neer op een toon die iets hoger lijkt te zijn.
Bij het voorbijrijden, wordt de naderende auto een zich verwijderende auto.
De golven doen er nu iets langer over. De toon lijkt nu lager.
De waargenomen frequentie bij een bewegende bron wordt:
bij naderen van het geluid
bij verwijderen van het geluid
In deze formules staat v voor de snelheid van het geluid.
Deze is afhankelijk van temperatuur en luchtvochtigheid, maar in een grootteorde van 335 m/s of 1200 km/u.
Een la van 440 Hz klinkt bij een naderingssnelheid van 100 km/u als 480 Hz, dat is iets tussen sib en si.
Een la van een verwijderende bron aan 100 km/u klinkt als 406 Hz, bijna zo laag als een sol.
Elke golf van de naderende auto doet er een welbepaalde tijd over om de waarnemer te bereiken.
De volgende golf moet een iets kleinere afstand afleggen, omdat de auto nu dichterbij is.
De waarnemer ontvangt de golven in een net iets hogere frequentie dan wanneer de auto stilstaat.
Dat komt neer op een toon die iets hoger lijkt te zijn.
Bij het voorbijrijden, wordt de naderende auto een zich verwijderende auto.
De golven doen er nu iets langer over. De toon lijkt nu lager.
De waargenomen frequentie bij een bewegende bron wordt:
bij naderen van het geluid
bij verwijderen van het geluid
In deze formules staat v voor de snelheid van het geluid.
Deze is afhankelijk van temperatuur en luchtvochtigheid, maar in een grootteorde van 335 m/s of 1200 km/u.
Een la van 440 Hz klinkt bij een naderingssnelheid van 100 km/u als 480 Hz, dat is iets tussen sib en si.
Een la van een verwijderende bron aan 100 km/u klinkt als 406 Hz, bijna zo laag als een sol.