Les quadrilatères particuliers
1°) Axes de symétrie des quadrilatères particuliers
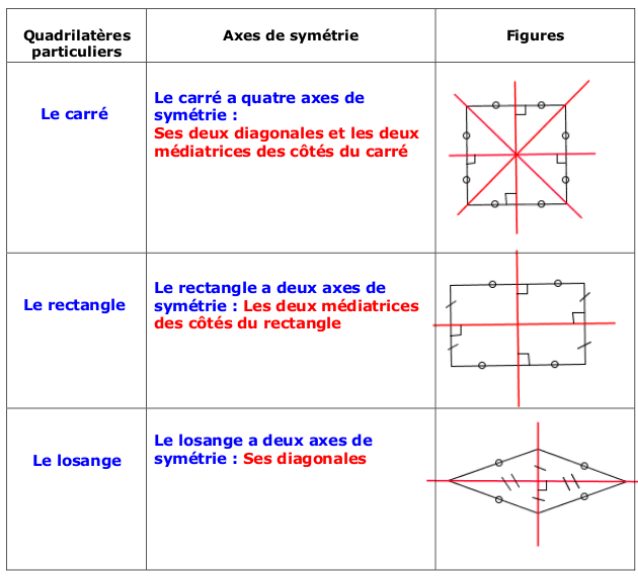
2) Conséquences : Propriétés des quadrilatères particuliers
a) Le rectangle
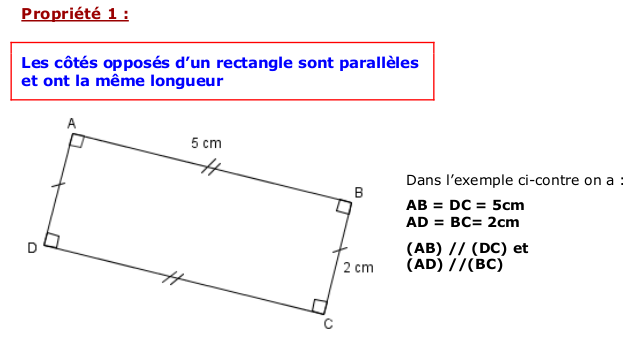
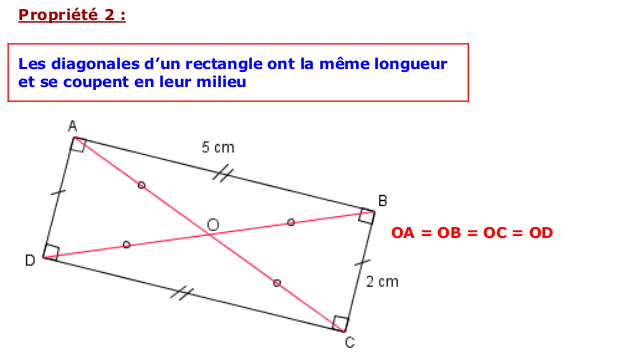
c) Le carré
b) Le losange

c) Le carré
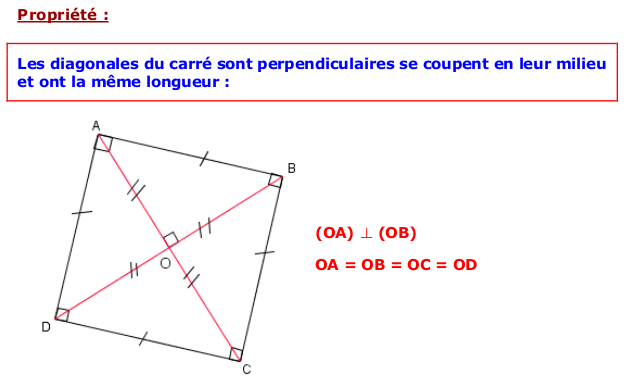
Remarque
Le carré est un rectangle particulier car il a ses quatre angles droits.
Le carré est aussi un losange particulier car il a ses quatre côtés de même longueur.