IM2.7 T5 Inscribed Triangles
In our earlier triangle investigations, you learned how to construct a circle containing the three vertices of a triangle. Use what you learned to construct circumcircles around the triangles below.
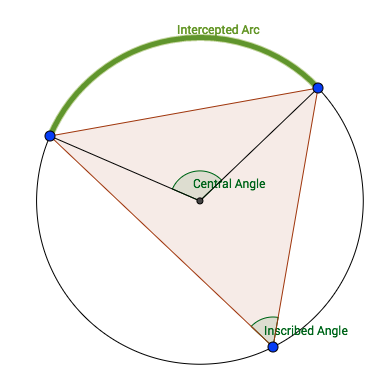
Since each vertex of an inscribed triangle lies on the circle, each angle of the triangle is an inscribed angle. We know that the sum of the measures of the interior angles of the triangle is 180° and that the sum of the measures of the three intercepted arcs is 360°. The degree measure of an arc is, by definition, the same as the measure of the central angle formed by the radii that contain the endpoints of the arc. But how is the measure of an inscribed angle that intercepts this same arc related to the measure of the central angle and the intercepted arc? That is something useful to find out. In your construction above, measure some central angles and inscribed angles, and try to come up with a rule relating them.