Flächeninhaltsfunktion

Gegeben ist die Funktion .
Es soll ein Verfahren entwickelt werden, wie man den Inhalt der Fläche zwischen Graph und -Achse im Intervall bestimmen kann.
Für jeden Wert von b kann man den Inhalt der Fläche zwischen dem Graphen von und der -Achse durch die Ober- und die Untersumme annähern.
Aber könnte man auch allgemein eine Funktion finden, die den Flächeninhalt zwischen Graph und -Achse im Intervall beschreibt?
Beachte die folgenden zwei Hinweise:
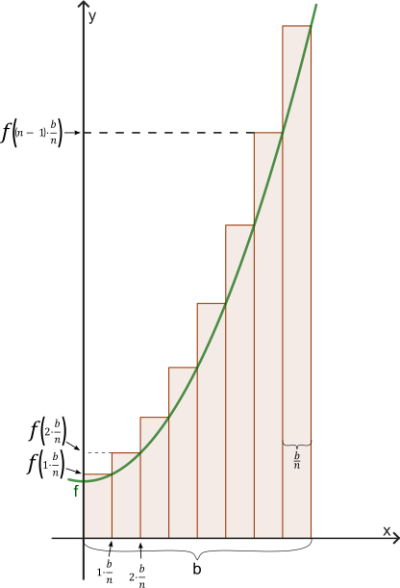
1. Der Flächeninhalt der Obersumme ist die Summe der Flächeninhalte der einzelnen Rechtecke, deren rechte oberen Ecken auf dem Graphen von liegen.
Die Breite der einzelnen Streifen beträgt jeweils bei Streifen.
Der Flächeninhalt des -ten Streifens ist daher Funktionswert an der Stelle .
2. Für die Summe der ersten Quadratzahlen gilt .
(Diesen Sachverhalt kann man mit vollständiger Induktion beweisen, siehe z.B. hier.)
Bringe im folgenden Applet die Terme in die richtige Reihenfolge, indem du an den Punkten ziehst und die Terme in den grauen Rechtecken positionierst.
Schalte dafür das Applet in den Vollbildmodus.
Anmerkung: die Berechnung des Flächeninhalts mit der Untersumme erfolgt analog und führt zum selben Ergebnis. Probiere es hier aus!
Welchen Zusammenhang vermutest du zwischen der Funktion und der Flächeninhaltsfunktion ?