Ecuación de la recta
Las rectas se pueden representar algebraicamente mediante ecuaciones lineales, es decir, tanto la variable independiente x como la variable dependiente y aparecen de forma lineal. Por ejemplo , son ecuaciones lineales, mientras que , no son lineales.
Es decir, una ecuación es lineal cuando el grado de las variables es como máximo 1.
En general, cualquier ecuación lineal siempre se puede escribir de la forma
y = mx + b
donde m se llama pendiente y b ordenada en el origen. Por ejemplo, en la recta y = 2x − 1,
2 es la pendiente y −1 es la ordenada en el origen. Geométricamente la pendiente representa la inclinación y la ordenada en el origen el corte con el eje y.
En caso de que la recta no esté expresada en esta forma, siempre se puede manipular
algebraicamente para obtener de manera sencilla la pendiente y la ordenada en el origen.
Ejemplo: Calcular la pendiente y la ordenada en el origen de la recta x − 3y = 2
Como la ecuación no está en la forma y = mx + b, es necesario despejar el valor de y.
Reescribiendo la ecuación se obtiene y = − , por tanto la pendiente es m = y la ordenada
en el origen b = −.
En las siguientes actividades indicar la pendiente de las rectas
Actividad 1
y=3x+1
Actividad 2
x+y=3
Desde el punto de vista geométrico, la pendiente indica la inclinación que tiene la recta. Si
la pendiente es positiva se tiene una recta creciente conforme aumenta x, y en caso que sea
negativa se tiene una recta decreciente conforme aumenta x.
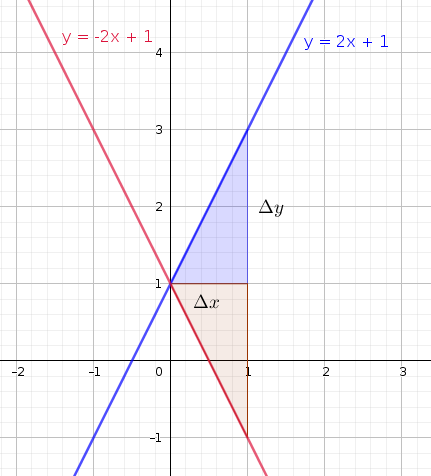
En la imagen a continuación se pueden ver dos rectas con el mismo valor de b pero con pendientes con el signo contrario. La recta de color azul tiene una pendiente de 2 mientras que la recta en rojo de -2.
La pendiente se puede calcular como el cociente de la variación en y sobre la variación en x. Es decir
donde y
Para ambas rectas se puede ver que en la zona sombreada , mientras que para la recta azul y para la roja . Entonces en la recta azul por cada variación de 1 en x se tiene una variación de 2 en y, mientras que en la roja por cada variación de 1 en x se tiene una variación de -2 en y.
En la siguiente hoja dinámica se puede modificar la pendiente m y la ordenada en el origen b de una recta usando los dos deslizadores.
Actividad 3
Utilizar la hoja dinámica para dibujar la recta y = 3x+1. ¿Cuál es la representación geométrica de la ordenada en el origen?
Actividad 4
Utilizar la hoja dinámica para dibujar la recta y=3x-2. Indicar el punto de corte de la recta con el eje y