Quatrefoil
The Cathedral of Burgos has mathematical foundations. The architects were aware of mathematics. The book "Teseros Matematicos de la Catedral de Burgos" explains the mathematics behind its architecture. The quatrefoil, for example, is a decorative element consisting of a symmetrical shape which forms the overall outline of four partially overlapping circles of the same diameter. The word 'quatrefoil' means "four leaves", from the Latin quattuor, "four", plus folium, "leaf".
See Instagram for my story
See: Wikipedia: Quatrefoil
Exercise 0
Start an image search on "quatrefoil gothic", collect and describe the results.
![Figure from "[i]Teseros Matematicos de la Catedral de Burgos[/i]" (page 97)](https://beta.geogebra.org/resource/xt25fnem/u2RJsxsqn4LHYcqY/material-xt25fnem.png)
Exercise 1
Let's start with the basic configuration before we move on to the figure of the book. Four circles fit in a square. Each of its sides touches two circles. Say the radius of the circles is 1. Proof that the perimeter of the square is 16 and the area of the square is also 16.

Exercise 2
Now, we draw another square whose sides are perpendicular to the diagonals of the inner square.
Proof that the area of the outer square is double the area of the inner square.
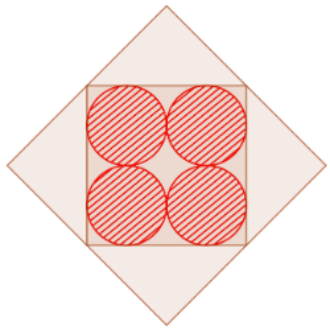
Exercise 3
Now we construct a smaller square, tangent to the four circles. The sides are perpendicular to the line passing the centers of two opposite circles. Say the radius of the circles is 1. Prove that the area of the square is , which is less than double of the area we started with..
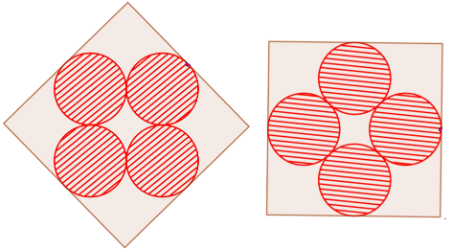
Exercise 4
More general, we can rotate the square in such a way that it remains the bounding box of the four circles. Say, the angle is . Say the radius of the circles is 1. Proof that the formula for the area of the square is . Proof that the area is minimal for . Investigate when the area is maximal.
Exercise 5
Say the radius of the circles is 1. Prove that the area of the quaterfoil is and that its perimeter is .