inflation and deflation

Penrose experimented witg grouping and division of kites and darts. This principle also yields for girih tiles. In the mausoleum of Maragha we see that the tiles beyond the clear zigzagging are divided themselves with lines slightly sticking out. This pattern too can be covered with a smaller pattern of girih tiles and match with a Penrose tiling.
We can clearly see the Penrose similarity on a multiple scale in the Darb-e Imam shrine in Isfahan.
Darb-e Imam shrine in Isfahan

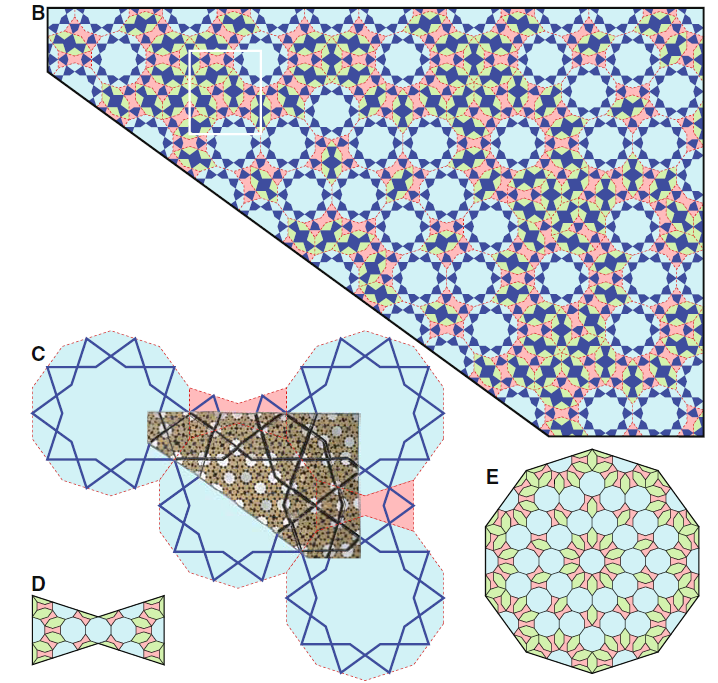
- C: Picture A fits in a giri pattern of 5 blue decagons and 2 pink bowties. The black lines in the pattern coincide with the blue zigzagging lines on the girih tiles.
- D and E: As in Penrose darts and kites you can draw a smaller pattern of girih tiles in each tile. D shows the subdivision of a bowtie, E the subdivision of a decagon.
- B: Applying these subdivisions to the pattern, we get a pattern that fits the smaller white, brown and black forms in it.
irregular or in fact regular?
When looking at the division of the poygonal pattern of the spandrel, you can understand the fascination of Lu and Steinhardt. As in Penrose tilings you see areas with local 5-fold symmetry and the decoration of the spandrel clearly doesn’t look regular at all. Did the decorators in 1200 already knew what Penrose discovered only in 1974? This claim raised many comments. In a next chapter we’ll respond to this comments.
remark by Peter Cromwell
One of the clearest comments came from Peter Cromwell in an article in Nexus Journal (2016) Peter Cromwell writes "the pattern is constructed by filling compartments and not by subdividing modules as has been previously suggested. None of the medieval patterns is quasiperiodic."
Het pattern of decagons and bow ties is a regular pattern as a frame to be filled up in a 2nd layer with polygonal forms from the same 5-fold system. These forms aren’t generated by a division rule as in Penrose tilings and don’t illustrate the principles of deflation and inflation.