Google Classroom구글 클래스룸
GeoGebra지오지브라 클래스룸
GeoGebra

Lines and Angles (Module 4)

저자:Katia Clouse
주제:각

G-CO.3.9

This activity gives students the opportunity to observe theorems [which] include: Vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are [exactly those] equidistant from the segment’s endpoints.

REMEMBER:

Complementary angles are angles whose measures have a sum of 90 degrees. Supplementary angles are angles whose measures have a sum of 180 degrees.

DEFINITION

DEFINITION
A linear pair is defined as angles having a common side, and whose noncommon sides form opposite rays. In the diagram above, Angle 1 and Angle 2 form a linear pair. When angles share a common side, they are adjacent.

In this diagram, which ray is the common side for the adjacent angles and ?

적용되는 모든 것을 선택하세요.
  • A
  • B
  • C
  • D
답안을 점검하세요 (3)

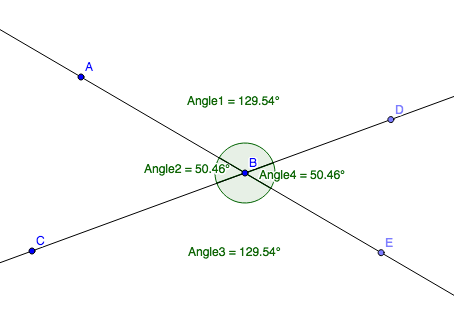
In the diagram below, click and drag points A and C to change the measures of the angles.

What do you notice is always true about the linear pair of angles?

적용되는 모든 것을 선택하세요.
  • A
  • B
  • C
  • D
답안을 점검하세요 (3)

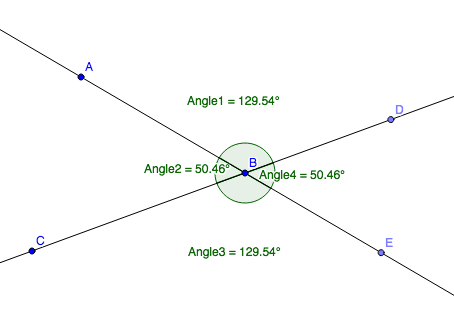
DEFINITION

DEFINITION
Vertical angles - nonadjacent angles formed by two intersecting lines. (Read: vertical angles do not have a common side)

In the diagram below, click and drag points A and C to change the measures of the angles.

What do you notice is always true about the vertical angles?

적용되는 모든 것을 선택하세요.
  • A
  • B
  • C
  • D
답안을 점검하세요 (3)

In the diagram above, which angles are vertical angles?

적용되는 모든 것을 선택하세요.
  • A
  • B
  • C
  • D
답안을 점검하세요 (3)

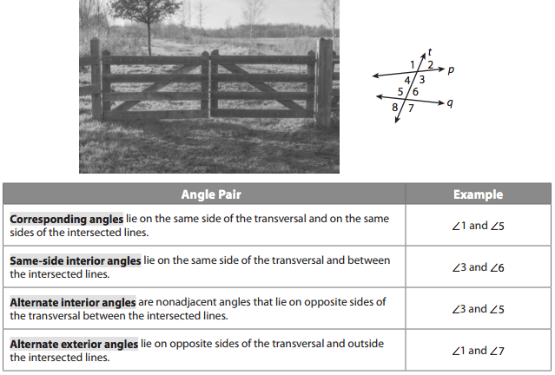
Note the kinds of angles formed by 2 lines p and q, and transversal t. This diagram is also in your text (p. 175).

Note the kinds of angles formed by 2 lines p and q, and transversal t. This diagram is also in your text (p. 175).
Here the two lines cut by a transversal are parallel. Click and drag point B to change the angle measures. Answer the questions below about what is ALWAYS true about these special angles when parallel lines are cut by a transversal.

Same-Side Interior Angles Postulate

If two parallel lines are cut by a transversal, then the same-side interior angles (like Angle Two and Angle Three) are

적용되는 모든 것을 선택하세요.
  • A
  • B
  • C
답안을 점검하세요 (3)

Corresponding Angles Theorem

If two parallel lines are cut by a transversal, then the corresponding angles (like Angle One and Angle Four) are

적용되는 모든 것을 선택하세요.
  • A
  • B
  • C
답안을 점검하세요 (3)

Alternate Interior Angles Theorem

If two parallel lines are cut by a transversal, then the alternate interior angles (like Angle One and Angle 3) are

적용되는 모든 것을 선택하세요.
  • A
  • B
  • C
답안을 점검하세요 (3)

What is line CD?

In the diagram below, which of the following provides the best description of line CD as it relates to segment AB?

적용되는 모든 것을 선택하세요.
  • A
  • B
  • C
  • D
  • E
  • F
답안을 점검하세요 (3)

Perpendicular Lines

Click and drag point D.

While the lengths are changing, is there anything that is always true?

적용되는 모든 것을 선택하세요.
  • A
  • B
  • C
  • D
답안을 점검하세요 (3)

새 자료

자료 찾기

주제 찾기