Geo-2017-Construction-Similar Triangles
AA Similarity Theorem
If two triangles have exactly two pairs of corresponding angles that are congruent, then the triangles are similar.
- Draw any triangle using the polygon tool at the top of the screen.
- Measure the lengths of each sides.
- Use the angle tool to measure the angles at each vertex.
- Construct the midpoint of the each side.
- Connect the midpoints to make a triangle.
- Measure the perimeter of each triangle using the following command:
Perimeter[poly1]
SAS Similarity Proof
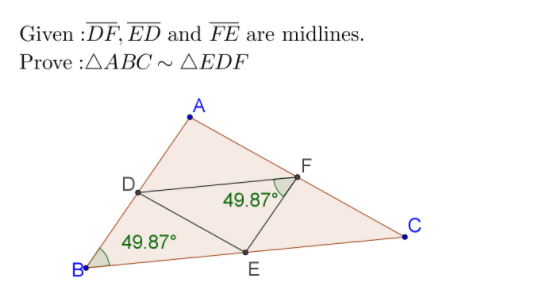
Prove that ABC and the triangle formed by its midlines [segments connecting the midpoints of each side] are similar.
Similar Triangles: Scale Ratio
1. Draw the triangle formed by the midpoints of the .
2. Measure the lengths of corresponding sides
3. Use the input bar to calculate the scale factor between and .
Similar Triangles: Scale Ratio
Prove that and the triangle formed by its midlines [segments connecting the midpoints of each side] are similar. [Hint: Notice any parallel lines, special triangles or quadrilaterals? ]
Analysis
What is the scale ratio of the new triangle to the original triangle ? Prove that the scale ratio will always be 2.