Google Classroom
GeoGebraGeoGebra Classroom
GeoGebra

QuarreLOTerals

Author:kateyvonneespiritu9
Hello Student! In this activity, you will investigate some similarities of square and rectangle, and square and rhombus. There are three special types of parallelograms namely rectangles, rhombuses, and squares. Each have the properties of parallelograms but is also unique in their own way. (Kalin & Corbitt, 1993) First, observe the vicinity map of your grandmother's lot and try to guess which one is your mother's lot, your auntie's lot, and your uncle's lot. Note that your mother's lot is square, your auntie's lot is rectangle, and your uncle's lot is rhombus.
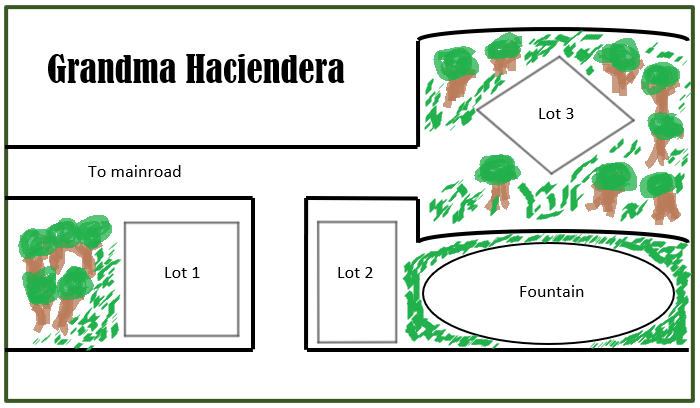
Image

Which one is your mother's lot?

Select all that apply
  • A
  • B
  • C
Check my answer (3)

Which one is your auntie's Lot?

Select all that apply
  • A
  • B
  • C
Check my answer (3)

Which one is your uncle's lot?

Select all that apply
  • A
  • B
  • C
Check my answer (3)
Now, it is time to investigate and find their similarities: Directions: 1. Use the Angle tool to measure the angles of the square - Click on point G, E, and F - Click on point E, F, and H - Click on point F, H, and G - Click on point H, G, and E 2. Use the Angle tool to measure the angles of the rectangle (do the same process) 3. Use the Angle tool to measure the angles of the rhombus (do the same process) Take note of your observation and answer the question below.

Which two among the three parallelograms have all interior angles equal to 90o?

Select all that apply
  • A
  • B
  • C
Check my answer (3)
Another investigation! Go back to the applet above (reset it first). Directions: 1. Use the Distance or length tool to measure the side lengths of the square - Click on line GE - Click on line EF - Click on line FH - Click on line HG 2.Use the Distance or length tool to measure the side lengths of the rectangle (do the same process) 3. Use the Distance or length tool to measure the side lengths of the rhombus (do the same process) Take note of your observations then answer the questions below.

Which two among the three parallelograms satisfies the property of having all four sides congruent?

Select all that apply
  • A
  • B
  • C
Check my answer (3)

How can you justify your grandmother's last testament that square and rectangle is somehow similar, and square and rhombus has also something in common using some of the properties of a square, rectangle, and rhombus?

Reference: Corbitt, M., & Kalin, R. (1995). Prentice Hall: Geometry: pp. 233. Anvil Publishing Incorporated

New Resources

Discover Resources

Discover Topics