Representación de números reales en la recta numérica
INTRODUCCIÓN
El conjunto está formado por números racionales () e irracionales. Dijimos anteriormente que es un conjunto continuo que se representa gráficamente sobre una recta numérica. A cada número real, tanto racional como irracional, le corresponde un punto en la recta y viceversa.
Aprenderemos a graficarlos utilizando Geogebra.
Introducción
Representación de números racionales
Representaremos números racionales en su expresión fraccionaria en la recta numérica.
Recordaremos el Teorema de Thales, en particular, una de sus aplicaciones la cual nos permitirá dividir cualquier segmento unitario en un número variable de segmentos congruentes.
Teorema de Thales:
Si tres o más rectas paralelas intersecan a dos o más rectas cualesquiera, determinan sobre éstas
segmentos proporcionales entre sí.
División de un segmento en n partes congruentes
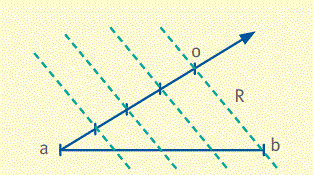
Representación números racionales
Representación Números irracionales
Teorema de Pitágoras

![[url=https://educrea.cl/wp-content/uploads/2018/07/guia-aprendizaje-geometria-y-trigonometria-1.pdf]https://educrea.cl/wp-content/uploads/2018/07/guia-aprendizaje-geometria-y-trigonometria-1.pdf[/url]](https://beta.geogebra.org/resource/vurd5tdj/igOQM1BEsiNw8gBP/material-vurd5tdj.png)