Progresiones aritméticas y geométricas
Introducción
Sin ser demasiado rigurosos, podemos definir una sucesión (o progresión) numérica como un conjunto de números ordenados. A cada uno de estos números los llamamos términos de la sucesión: es el primer término, es el segundo término, es el tercer término... es el n-ésimo término.
Ejemplos:
- Sucesión de los números pares: 2, 4, 6, 8, 10, ...
- Sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, 13,...
Sucesión aritmética
Cada término se obtiene sumando un número, , al término que le precede. El número se llama diferencia de la sucesión.
Por ejemplo, en la sucesión de los números pares, la diferencia es d = 2.
La diferencia se calcula restando dos términos consecutivos:
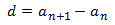Conociendo el primer término y la diferencia, podemos calcular el término :
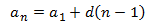
Suma de los primeros términos:
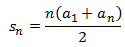
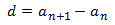Conociendo el primer término y la diferencia, podemos calcular el término :
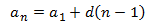
Suma de los primeros términos:
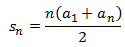
Sucesión geométrica
Un una sucesión geométrica, cada término se obtiene multiplicando por al término que le precede. El número se denomina razón.
Por ejemplo, la razón de la sucesión 2, 4, 8, 16,... es r = 2.
La razón se calcula dividiendo dos términos consecutivos:
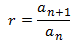El término general es
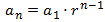
La suma de los primeros términos es
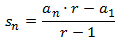
Además, si , la suma de los infinitos términos de la sucesión es
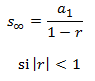
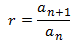El término general es
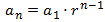
La suma de los primeros términos es
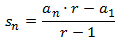
Además, si , la suma de los infinitos términos de la sucesión es
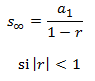
Otros recursos:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente