A légy-piszok
Feladat:
Legyen A, B,C, D a sík négy pontja, E az AB és CD egyenesek metszéspontja,és F a sík egy további pontja!
Vegyük fel az (F,E) egyenest!
Arra kérem olvasóimat, hogy az alábbi feladatot előbb a saját gépükre telepített Geogebra programmal oldják meg, majd csak ezt követően tegyék meg ugyanezt az alábbi (üres) appleten.
Ha a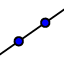 
ikont kiválasztva kezdjük a munkát, a rajzlap két pontjára kattintva máris megrajzoltuk az AB,
majd, ugyanígy a CD egyenest, Ezzel: 
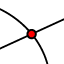megkaphatjuk E-t, végül legyen ismét 
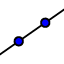az aktív ikon, a sik egy "üres" pontjára kattintva már csak (??) meg kell keresnünk E-t és rákattintunk. Készen vagyunk.
Rutinosabb felhasználók tudják, hogy a ikon kihagyható, elég, ha utolsó lépésként rákattintunk a két egyenes (látható) metszéspontjára. Ezzel máris megkaptuk E-t még egy kattintás a rajzlapra, és kész.
Csakhogy mi történik, ha "véletlenül" sietségből, figyelmetlenségből mellé kattintottunk?
Na, ez a légysz.. légy piszok a programozói szlengben! Gyakran megesik. Láttam már igényes szakmai cikk mellékleteként csatolt GeoGebra fájlban is.
Ez különösen akkor zavaró, ha van egy bonyolultabb "jól" elkészített ábránk, amelyet azonban ha megmozdítunk (miért ne tennénk: ezért dinamikus geometria), összeomlik az egész struktúra. Több, mint egy jó kövér helyesírási hiba. Ezzel értelmét veszti az egész rajz.
Ezt azzal lehet biztonságosan elkerülni, ha az összes olyan ikon, amelynek pont a bemenő adata, csak már előre felvett (megszerkesztett) pontot fogad el bemenő adatként.
Lehet, hogy így valamivel lassabbá válik a munka, de a biztonság miatt megéri. Próbálják ki.
ikont kiválasztva kezdjük a munkát, a rajzlap két pontjára kattintva máris megrajzoltuk az AB,
majd, ugyanígy a CD egyenest, Ezzel: megkaphatjuk E-t, végül legyen ismét az aktív ikon, a sik egy "üres" pontjára kattintva már csak (??) meg kell keresnünk E-t és rákattintunk. Készen vagyunk.
Rutinosabb felhasználók tudják, hogy a ikon kihagyható, elég, ha utolsó lépésként rákattintunk a két egyenes (látható) metszéspontjára. Ezzel máris megkaptuk E-t még egy kattintás a rajzlapra, és kész.
Csakhogy mi történik, ha "véletlenül" sietségből, figyelmetlenségből mellé kattintottunk?
Na, ez a Üres
A fenti rajzlap valóban üresnek tűnik. Csak egy jelölőnégyzetet tartalmaz, amely bármikor jól jöhet, ha ideiglenesen ki szeretnénk kapcsolni a szerkesztővonalainkat.
Azonban a Jobb-klikk\tulajdonságok\sript\globálisJavascript útvonalon eljuthatunk eddig a
function ggbOnInit() {
ggbApplet.setOnTheFlyPointCreationActive(false);
}
"varázsigéig" amit elegendő a legelső objektumba beírni, - ez itt megtörtént - ettől kezdve bele kerül minden továbbiba, és az imént tapasztalt jelenséget eredményezi. Megéri. Erősen javaslom.
Ha már itt tartunk...
... és megrajzolták a kért 6 pontból és 3 egyenesből álló rajzot. felhívom a figyelmüket a GeoGebra még egy sajátosságára.
Kapcsolják be a rácsot, állítsák be az A, B, C, D pontokat úgy, hogy AB ∥ CD teljesüljön. Ekkor az E pont "elvileg" nem létezik, az algebra ablakban is csak egy ? jelenik meg a neve mellett. Az FE egyenest mégis megrajzolja a GeoGebra. Ezzel eljuthatunk a projektív geometria végtelen távoli pontjának a fogalmához, mi több: használni is tudjuk.