Triangle Similarity Theorems Activity: Fix it Felix!
The Situation:
Suppose that you are a car mechanic. Your job is to fix your customer's car so they can safely drive around the city. One day, one customer enters your shop to have his car repaired.
You will use triangle similarity theorems to accomplish your task.
You will repair the customer's car part-by-part by accomplishing the tasks. You will use the appropriate tools (triangle similarity theorems) in order to successfully finish the tasks below.

Instructions:
Task # 1
Which among the three parts is similar to the triangle on the left?
Which tool are you going to use to fix this part? Explain how this theorem is applicable in this problem.
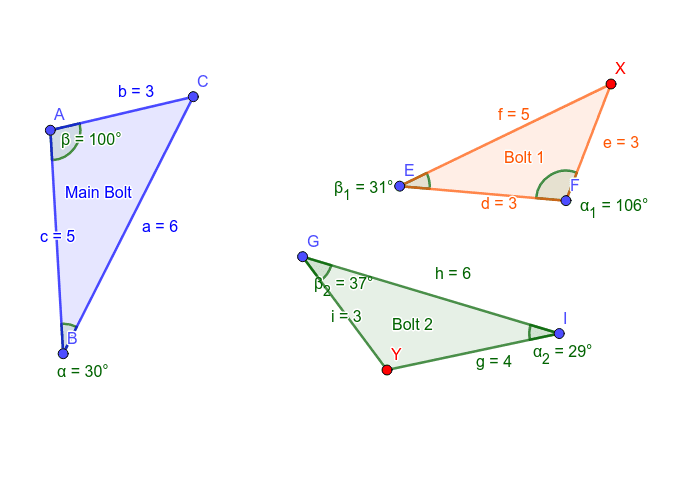
Under the hood, you see the following objects:
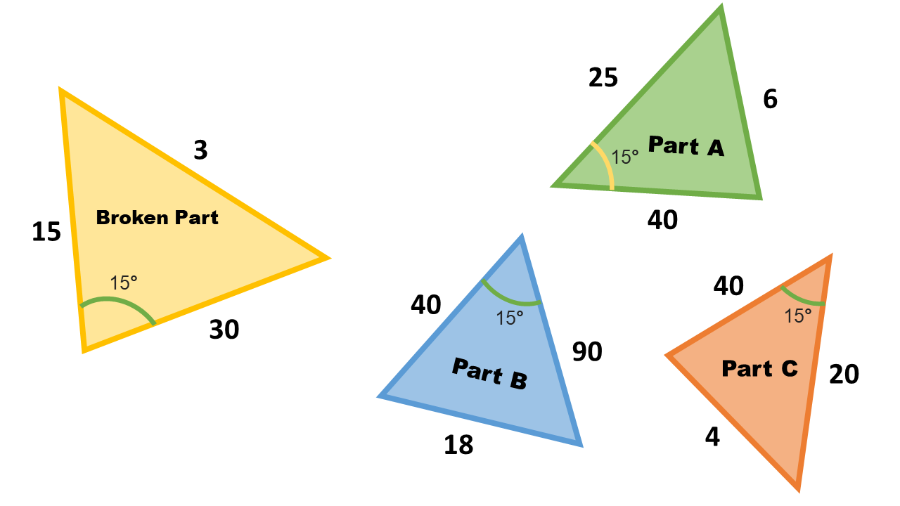
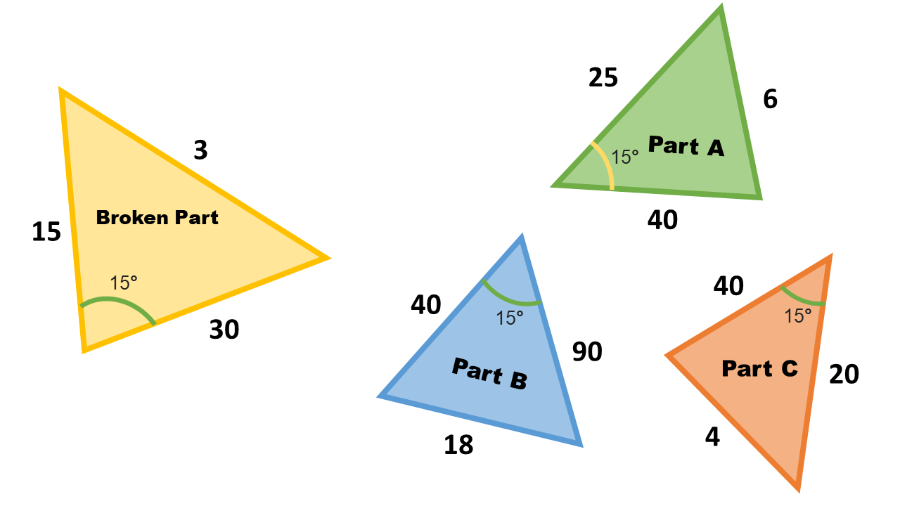
Below the midsection of the car, you see the following:
After fixing the first part, you look at the second portion of the car. You notice that the transmission needs some tweaking. Your task is to adjust the bolts on the right to make it similar with the main bolt at the left.
Task #2
What did you consider to make the bolts similar to the main bolt? What are the measurements of the sides opposite to the angles highlighted in green after adjusting the bolts?
Which tool did you use to fix the problem? What did you observe after manipulating the parts?
(Use the red points to manipulate the bolts)
You zoom in closer on the slot where the brake light is supposed to go and you see the following:
Finally, you check the rear part of the car for damages. You see that one of the brake lights are broken. You intend to 'install' the new brake light onto the slot to finish up the repairs. Your task is to compare a set of triangles and determine which brake lights are viable for installation.
Task #3
Observe all the triangles and compare the brake lights with the slot by dragging it over the slot. What can be inferred about measure angle X, Y, and Z? What can be inferred about their adjacent sides? Using this reasoning, which brake lights are similar to the slot?
