Kapitel
Theorems with almost no hypotheses
I'm interested in theorems which appear to have very few, if any hypotheses. Essentially a search for unexpected regularity or pattern in a relatively unstructured situation.
By "few hypotheses" I mean theorems which start "take any triangle", or "take any three circles". Similarly, the conclusion of the theorem ought to be really surprising. I know this is a little vague, but I've deliberately left it that way.
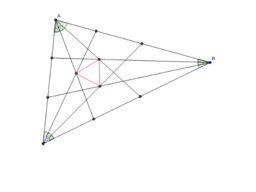
Perhaps my favourite here is Morley's theorem. This applies to *any* triangle, but has a very surprising conclusion. Contrast this with Pythagoras' theorem (needs a right angled triangle: too special!) or Viviani's Theorem (needs an equilateral triangle: too special!).
Can you help me gather a collection, together with their proofs?
Plane geometry
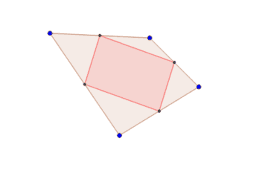
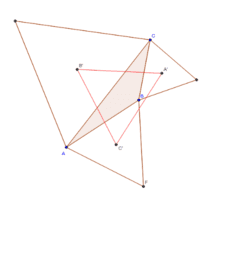
Theorems in plane geometry with few hypotheses.