Ecuación de la elipse
La elipse es una figura geométrica cerrada y simétrica en forma de óvalo. Es una de las cuatro secciones cónicas, junto con la circunferencia, hipérbola y parábola.
Matemáticamente, se define como el conjunto de todos los puntos en un plano para los cuales la suma de las distancias desde esos puntos a dos puntos fijos, llamados focos, es constante. Esta constante se denomina longitud focal.
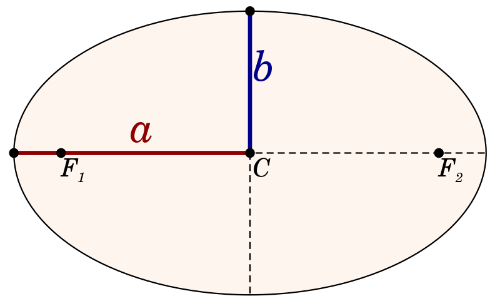
La elipse corta el eje que contiene los focos, F1 y F2 en dos vértices. El segmento que une los dos vértices pasando por el punto medio C se llama eje mayor de la elipse y tiene longitud 2a.
Además del eje mayor, la elipse también tiene un eje menor perpendicular al eje mayor. La longitud del eje menor se representa como 2b y es la distancia más corta entre los dos puntos de la elipse pasando por su centro.
La ecuación general de una elipse con centro en el origen (0,0) es
donde a y b son los semiejes mayor y menor respectivamente.
En caso de que ambos semiejes sean iguales, a=b=R se obtiene la ecuación de una circunferencia de radio R
En la siguiente hoja dinámica se puede ver la interpretación geométrica de los dos semiejes de la ecuación de la elipse.
Actividad 1
Comprobar que si los dos semiejes tienen el mismo valor se obtiene una circunferencia de radio a
Actividad 2
¿Qué sucede si el semieje mayor a es menor que el semieje menor b?
Excentricidad de una elipse
La excentricidad de una elipse es una medida que describe lo alargada o aplanada es la forma de la elipse en relación con un círculo perfecto. Depende de los valores del semieje mayor a y del semieje menor b mediante la seguiente relación
La excentricidad puede variar entre 0 y 1. Si la excentricidad es igual a 0, la elipse se convierte en un círculo perfecto, ya que sus semiejes son de igual longitud. A medida que la excentricidad se acerca a 1, la elipse se vuelve cada vez más alargada en una dirección, lo que significa que el semieje mayor es significativamente más largo que el semieje menor.
Actividad 3
Calcular la excentricidad de una elipse con semiejes a=4 y b=2
En la siguiente hoja dinámica se puede ver la interpretación geométrica de la excentricidad de una elipse
Actividad 4
Utilizar la hoja dinámica anterior para dibujar: a) una elipse con excentricidad e=0.8 b) una elipse con excentricidad e=0