Solución general de una EDO lineal de segundo orden
Una ecuación diferencial lineal homogénea y de segundo orden se representa así:
Siendo y los que determinan el comportamiento de la solución general, ya que afectan la forma de la ecuación característica asociada.
Resolución
Para resolver la ecuación, se asume una solución de la forma donde solamente está pendiente determinar el valor o valores de "m". Sustituyendo en la ecuación diferencial se obtiene la ecuación característica:
es justamente de esta ecuación cuadrática de donde podemos obtener los valores de "m" pero recordemos tambien que estas soluciones , pueden ser:
* Reales y diferentes entre si (en este caso el discriminante es mayor que cero )
* Reales e iguales entre si (en este caso el discriminante es igual a cero )
* Complejas y conjugadas (en este caso el discriminante es menor que cero )
Es importante identificar la naturaleza de las raíces de la ecuación cuadrática pues depende de ello para determinar la solución general de la EDO.
A continuación se presentan dos ejemplos en las cuales la ecuación característica tiene discriminante positivo (sus raíces son reales y diferentes entre sí) y por lo tanto la solución general tiene una forma general específica, sin embargo podrá notar que el hecho de que las raíces sean positivas o negativas impacta directamente en el comportamiento de la solución general.
Ejemplo 1. Resuelve la ecuación diferencial:
Como se señaló en el párrafo anterior, asumimos una solución de la forma .
La ecuación característica es: la cual al resolver obtenemos que: y
Observe también que para la ecuación característica, el discriminante es positivo: lo cual corresponde con el hecho de las raíces de la cuadrática son reales y diferentes entre sí.
Podemos observar que la solución propuesta puede ser y además son linealmente independientes, entonces por el principio de la superposición podemos obtener la solución general como la combinación lineal de las dos soluciones obtenidas, asi:
siendo ,
A continuación se muestra la gráfica de esta solución general, para determinados valores de y .
(Actualiza la gráfica dándole clic en el botón actualizar)
Gráfica de la solución general del ejemplo 1
Interpretación
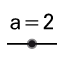, puede cambiar los valores de las constantes y y siempre la solución general mantiene el comportamiento decreciente cuando "t" tiende al infinito.Ejemplo 2. Resuelve la ecuación diferencial:
La ecuación característica es: la cual al resolver obtenemos que: y
Observe también que para la ecuación característica, el discriminante es positivo: lo cual corresponde con el hecho de las raíces de la cuadrática son reales y diferentes entre sí, similar al ejemplo 1.
Podemos observar que la solución propuesta puede ser y además son linealmente independientes, entonces, nuevamente por el principio de la superposición podemos obtener la solución general como la combinación lineal de las dos soluciones obtenidas, asi:
siendo ,
A continuación se muestra la gráfica de esta solución general, para determinados valores de y .
Observa en la gráfica como la solución general tiene un crecimiento exponencial, diferente al resultado del ejemplo 1. ¿Puedes explicar a que se debe esto?
En la siguiente gráfica tambien puedes usar los deslizadores para ver el resultado de la solución general para distintos valores de los coeficientes y pero notaras que la gráfica siempre mantiene un comportamiento creciente cuando "t" tiende al infinito.
(Actualiza la gráfica dándole clic en el botón actualizar)
para ver el resultado de la solución general para distintos valores de los coeficientes y pero notaras que la gráfica siempre mantiene un comportamiento creciente cuando "t" tiende al infinito.
(Actualiza la gráfica dándole clic en el botón actualizar)Gráfica de la solución general del ejemplo 2
Casos adicionales: cuando el discriminante es cero o negativo
En los dos ejemplos anteriores hemos visto el caso donde el discriminante es positivo. Pero tambien puede ocurrir que:
* El discriminante es igual a cero, es decir, las raíces de la ecuación característica son reales e iguales entre si.
En este caso la solución general de la ecuación diferencial adoptará la siguiente forma general: siendo "m" la raíz de multiplicidad 2 de la ecuación característica.
* El discriminante es negativo, es decir, las raíces de la ecuación característica son complejas y conjugadas.
En este caso la solución general de la ecuación diferencial adoptará la siguiente forma general: siendo y componentes de la raíz compleja de la ecuación característica.
A continuación veremos en el ejemplo 3 el caso cuando el discriminante es igual a cero y en el ejemplo 4 cuando el discriminante es negativo.
Ejemplo 3. Resuelve la ecuación diferencial:
La ecuación característica es: la cual al resolver obtenemos que: y
Observe también que para la ecuación característica, el discriminante es igual a cero: lo cual corresponde con el hecho de las raíces de la cuadrática son reales e iguales entre sí.
Como se señaló anteriormente, para este caso la solución general tiene la forma:
siendo , además como entonces
Reemplazando los valores, la solución general de esta ecuación diferencial es:
A continuación se muestra la gráfica de esta solución general, para determinados valores de y .
Observa en la gráfica como la solución general presenta un decrecimiento cuando "t" tiende al infinito. ¿Puedes explicar a que se debe esto?
(Actualiza la gráfica dándole clic en el botón actualizar)
Gráfica de la solución general del ejemplo 3
Ejemplo 4. Resuelve la ecuación diferencial:
La ecuación característica es: la cual al resolver obtenemos que: y
Observe también que para la ecuación característica, el discriminante es igual a cero: lo cual corresponde con el hecho de las raíces de la cuadrática son complejas y conjugadas.
Como se señaló anteriormente, para este caso la solución general tiene la forma:
siendo , además como entonces
Luego tenemos que y
Reemplazando los valores, la solución general de esta ecuación diferencial es:
A continuación se muestra la gráfica de esta solución general, para determinados valores de y .
Observa en la gráfica como la solución general presenta un crecimiento cuando "t" tiende al infinito. ¿Puedes explicar a que se debe esto?
(Actualiza la gráfica dándole clic en el botón actualizar)
Gráfica de la solución general del ejemplo 4
PREGUNTA 1
¿Por qué para la EDO lineal de segundo orden se asume que tiene solución de la forma ?
PREGUNTA 2
¿Cómo influyen los coeficientes a, b, c en la solución general?
PREGUNTA 3
Cuando el discriminante es positivo, pero las raíces son de diferente signo, ¿cómo es el comportamiento de la solución general?
PREGUNTA 4
Al resolver la ecuación diferencial encontramos que el discriminante de la ecuación característica es:
PREGUNTA 5
Al resolver la ecuación diferencial encontramos que el discriminante de la ecuación característica es: