Interpretación geométrica de la ecuación vectorial de la recta y del plano
Representación gráfica de la ecuación vectorial de la recta (Figura estática)
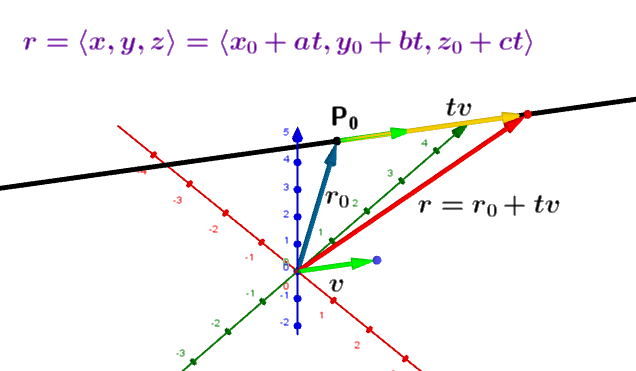
Ecuación vectorial de la recta con GeoGebra: Ecuación de la recta en el espacio, dados un punto y un vector director (Representación dinámica)
Detalle de los elementos geométricos en la vista gráfica 3D
1. El vector (verde) director es
2. El vector de posición (azul) de es .
3. El vector blanco es .
4. El vector (rojo) de posición es la ecuación vectorial de la recta.
5. El vector se puede variar moviendo el punto negro . Asimismo el vector director se puede cambiar de tamaño animando el punto azul.
6. Para desactivar el rastro o actualizar la construcción de clic en la esquina superior derecha en las dobles fechas.
Esta construcción está inspirada en el libro de tercero de bachillerato general unificado (texto integrado: https://recursos2.educacion.gob.ec/textos/) correspondiente a matemáticas para la aplicación de la TIC en matemáticas en las páginas 66-67 (aquí existe otra propuesta de construcción aplicando GeoGebra)
Teoría

Interpretación geométrica de la ecuación vectorial del plano (Figura estática)
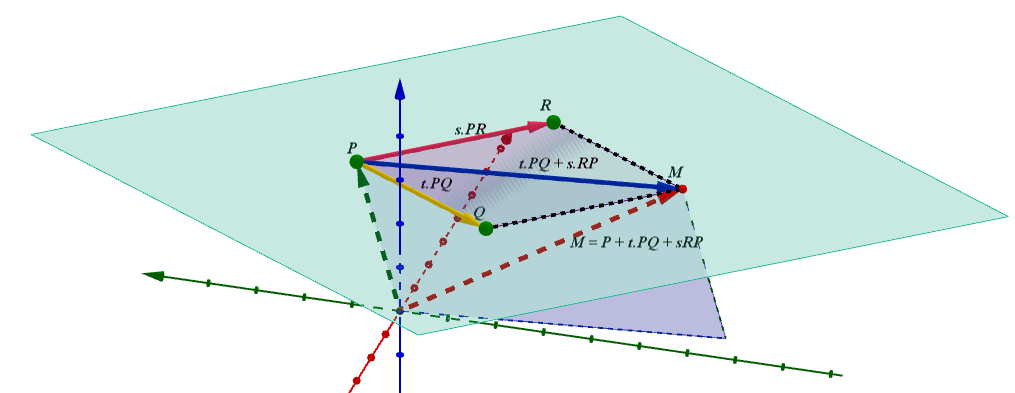
Detalle de los elementos geométricos en la vista gráfica 3D
1. El vector (rosa) es .
2. El vector (amarillo) es .
3. El vector (azul) es .
4. El vector (verde) es .
5. El vector (rojo) es .
Pregunta 1.
Explique ¿por qué al mover los puntos y los puntos rojos trazados por el vector de posición pertenecen al plano celeste?
Pregunta 2.
¿Qué concepto vectorial está involucrado en la expresión ?
Pregunta 3.
¿Cómo se obtiene la expresión ?
Pregunta 4.
Explica cómo se deduce la ecuación vectorial del plano.

