L6.11 - Perpendicular Lines in the Plane
Learning Intentions and Success Criteria
- Prove the slope criterion for perpendicular lines and use it to solve geometric problems.
- Prove that the slopes of perpendicular lines are opposite reciprocals.
- Use slopes of perpendicular lines to solve problems.
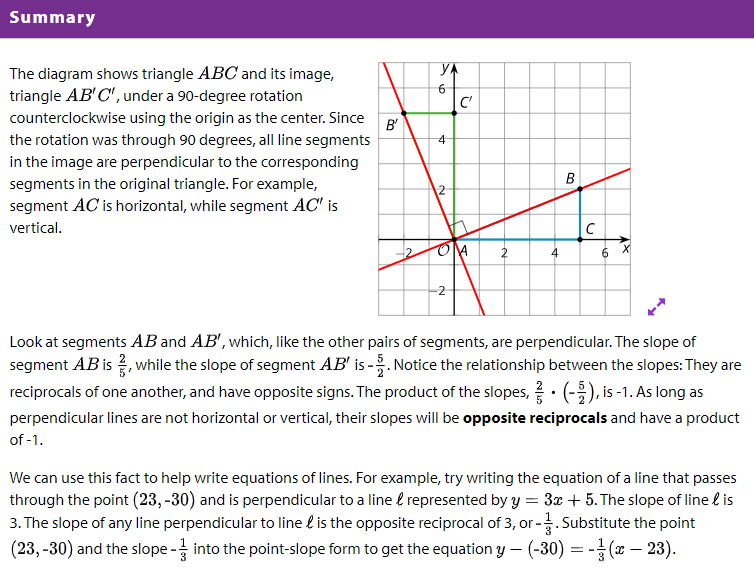
11.1: Revisiting Transformations
The image shows quadrilateral ABCD. Apply the transformation rule (x, y) → (-y, x) to quadrilateral ABCD. What is the effect of the transformation rule?
11.2: Make a Conjecture

1. Complete the table with the slope of each segment from the warm-up. lines segment original figure slope image slope product
lines segment original figure slope image slope product
lines segment original figure slope image slope product
lines segment original figure slope image slope product
2. The image in the warm-up is a 90-degree rotation counterclockwise of the original figure, so each line in the original figure is perpendicular to the corresponding line in the image. Use your slope calculations to make a conjecture about slopes of perpendicular lines.
11.3: Prove It
Let’s prove our conjecture about slopes of perpendicular lines for the case where the lines pass through the origin. 1. Find the slope of a line passing through the point (a, b) and the origin. Assume the line is not horizontal or vertical.
2. Suppose the line is rotated using the transformation rule (x, y) → (-y, x). Find the coordinates of the images of the points (a, b) and the origin.
3. How does the original line relate to the image?
4. Find the slope of the image.
5. Compare your slopes. What did you just prove?
Lesson Synthesis: Perpendicular Lines in the Plane
1. Write an equation for any line perpendicular to line n.
Learning Intentions and Success Criteria
- Prove the slope criterion for perpendicular lines and use it to solve geometric problems.
- Prove that the slopes of perpendicular lines are opposite reciprocals.
- Use slopes of perpendicular lines to solve problems.
Cool-Down: Another Perpendicular Line
Write an equation of the line that passes through (-4, 1) and is perpendicular to the line y = 2x + 3.


