Calculando las transiciones
Esta actividad pertenece al libro de GeoGebra Inclinando la botella de Piaget con GeoGebra Discovery.
Una vez analizados los cuatro casos, pasaremos a integrarlos en una única construcción. Para ello, debemos considerar el orden en que el nivel del líquido alcanza las diferentes bases.
Sea t la tangente del ángulo de inclinación de la botella α=Ángulo(A',A,U): t = tg(α).
Si la botella está llena igual o menos de la mitad se alcanzará la base inferior cuando t = 2 AH / AA' = 2h/b, tal como muestra la siguiente imagen.
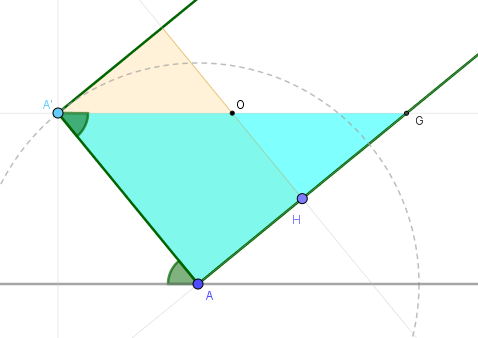
Si la botella está llena igual o más de la mitad se alcanzará la base superior cuando t = D'G' / AA' = 2 DH / AA' = 2(a-h)/b, tal como muestra la siguiente imagen.
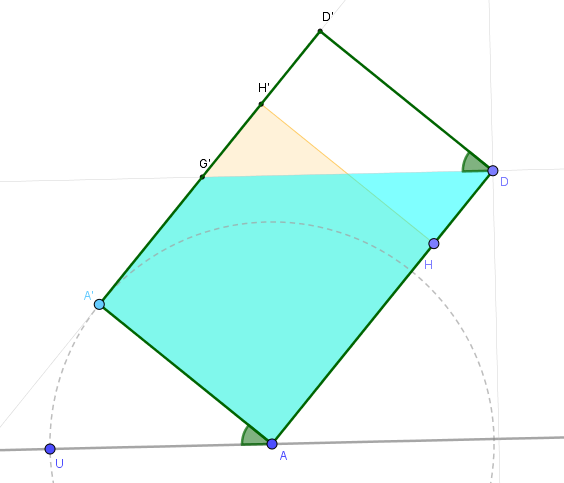
Cuando la botella esté llena igual o menos de la mitad se alcanzarán ambas bases cuando F = D. En ese momento, t = AD / AE, tal como muestra la siguiente imagen. Como sabemos que AE AF = 2 AA' AH, tenemos:
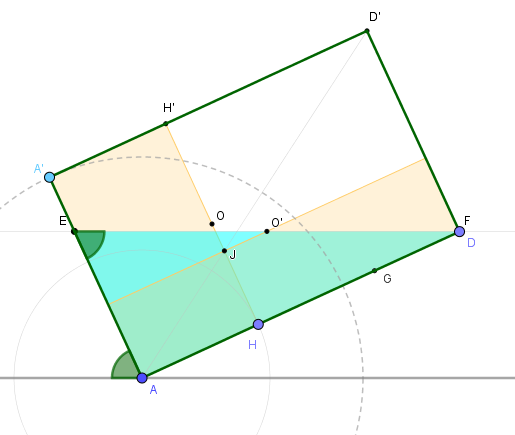
Finalmente, por simetría respecto a la imagen anterior, cuando la botella esté llena igual o más de la mitad se alcanzarán ambas bases cuando: