Test jezelf
Vraag 1
Dit is een deel van de grafiek van een functie.
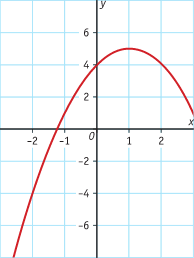
Teken bij deze grafiek een toenamediagram met stapgrootte 1, te beginnen bij x = - 2.
Vraag 2
Schets een toenamediagram bij een grafiek die:
a. constant stijgt
b. afnemend daalt
c. toenemend stijgt
Vraag 3
Gegeven is de functie f met voorschrift f(x) = 0,5x4−4x2+8.
a. Met de grafische rekenmachine kun je de grafiek van deze functie bekijken en in je schrift een toenametabel maken. Teken een toenamediagram op het interval [-3,3] met een stapgrootte van 0,5. Rond af op één decimaal nauwkeurig.
b. Hoe zie je aan het toenamediagram dat er precies één interval is waarop de grafiek toenemend daalt?
c. Waarom kun je op grond van het toenamediagram concluderen dat er in ieder geval drie extremen zijn?
Vraag 4
Bekijk de grafiek van de gemiddelde dagtemperatuur en het bijbehorende toenamediagram met stapgrootte 2.
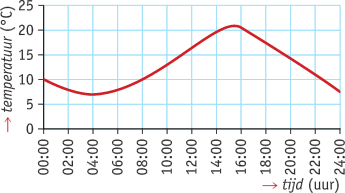
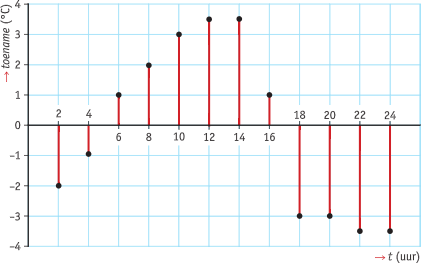
a. Op welk interval is de temperatuur stijgend?
b. Hoe kun je dat zien aan de grafiek?
c. Hoe kun je dat zien aan het toenamediagram?
d. Op welk interval is de temperatuur dalend?
e. Hoe kun je dat zien aan de grafiek?
f. Hoe kun je dat zien aan het toenamediagram?
g. Wanneer je naar de grafiek kijkt, lijkt het erop dat er op het interval <8,12> sprake is van een constante stijging. Leg uit dat dit niet waar is door gebruik te maken van de informatie in het toenamediagram.
h. Op welk interval is er sprake van een constante daling? Licht je antwoord toe.
Vraag 5
a. Een toenamediagram met stapgrootte Δx = 1 van een lineaire grafiek bestaat uit allemaal staafjes die 2 hoog zijn. Verder is gegeven dat de bijbehorende grafiek door het punt (0,5) gaat. Stel de formule op bij de grafiek die hoort bij het toenamediagram.
b. Een toenamediagram met stapgrootte Δx = 4 van een lineaire grafiek bestaat uit allemaal staafjes die - 8 hoog zijn. Verder is gegeven dat de bijbehorende grafiek door het punt (2,3) gaat. Stel de formule op bij de grafiek die hoort bij het toenamediagram.