Voorbeeld en opgaven 30, 31 en 32
Voorbeeld
Bekijk de grafiek van de functie f met voorschrift f(x) = 0,5x4 − 4x2.
Teken de grafiek van de bijbehorende hellingsfunctie f'.
Oplossing
Maak eerst met behulp van de grafische rekenmachine een tabel met hellingsgetallen:

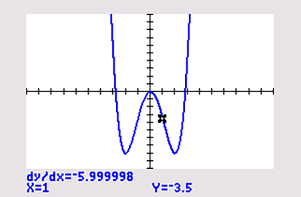
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| -30 | 0 | 6 | 0 | -6 | 0 | 30 |
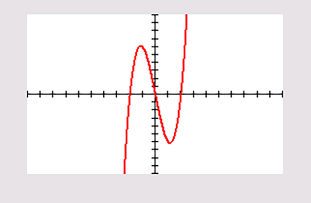
Je kunt ook direct de grafische rekenmachine de hellingsgrafiek laten tekenen. Gebruik de optie nDeriv uit het MATH-8 om de hellingfunctie te plotten.
Opgave 30
Bekijk de grafiek van f(x) = 0,5x3 − 6x.
a. Maak met je rekenmachine de grafiek van f'(x).
b. Bepaal f'(1). Stel een vergelijking op van de raaklijn aan de grafiek van f voor x = 1.
c. Bereken met de grafische rekenmachine het minimum van f. Laat de grafische rekenmachine vervolgens het rechter nulpunt van f' berekenen. Als het goed is, vind je beide keren ongeveer dezelfde waarde van x. Waarom is dat zo? En waarom is dat "ongeveer"?
Opgave 31
Gegeven is de grafiek van f(x) = 3x2 − 7.
a. Bepaal het differentiaalquotiënt bij de gegeven tabel. Je kunt hiervoor je GR gebruiken.
b. Teken met de gevonden gegevens de hellingsgrafiek.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Opgave 32
Voor een bewegend voorwerp geldt s(t) = 1,2t2 waarin s de afgelegde afstand in meter en t de tijd in seconden is.
a. De snelheid van dit voorwerp na vijf seconden is s'(5). Bereken deze snelheid in m/s en in km/h.
b. De snelheid v is een functie van t, de hellingsfunctie s'(t). Teken de grafiek van v.
c. Stel een functievoorschrift op voor v(t).
d. Na hoeveel seconden beweegt het voorwerp met een snelheid van 50 km/h? (Rond af op één decimaal.)