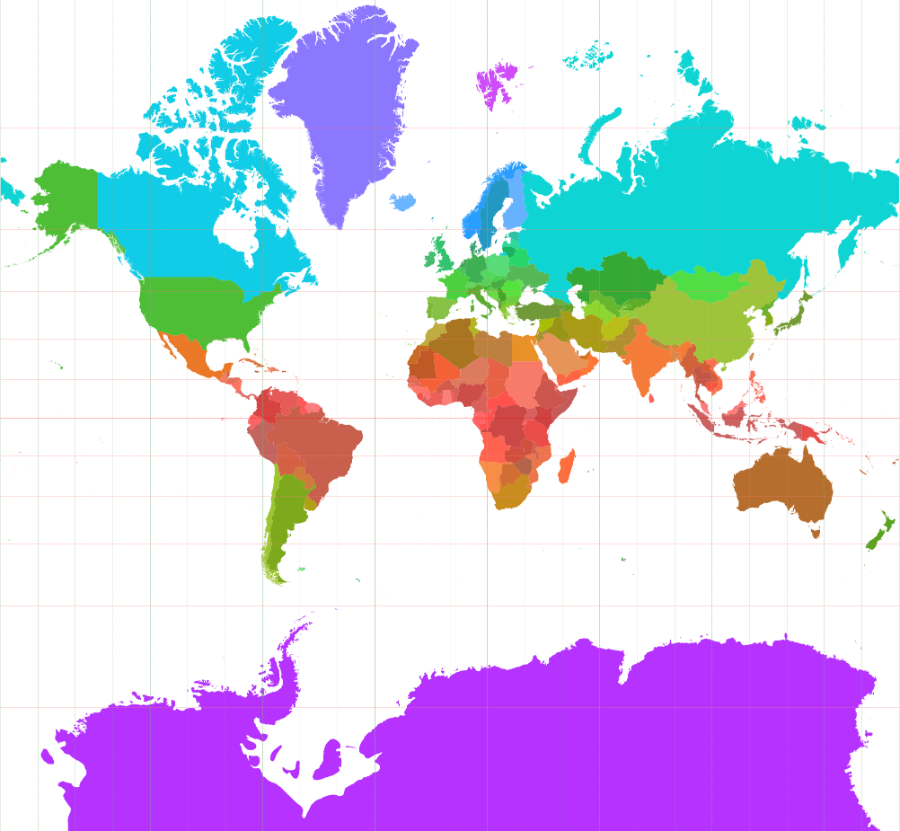
hoekgetrouwe kaartprojecties
waarom?
Je kunt een kaart zo maken dat de vervormingen minimaal lijken, dat de oppervlaktes overeenkomen of dat volgens bepaalde lijnen de afstanden kloppen. Maar waarom zou je een kaart willen maken die hoekgetrouw is? De vraag naar dergelijke kaarten kwam vanuit de navigatie en had een groot nut. Het is namelijk heel praktisch dat je voor elk mogelijke route gewoon je gradenboog op de kaart kunt leggen om je kompaskoers te bepalen. Alleen was dat gemakkelijker gezegd dan gedaan.
Gerard Mercator slaagde in het opzet in 1569 met zijn wereldkaart Nova et aucta orbis tarrae descriptio ad usum navigantium emendate accommodata (nieuwe en actuele beschrijving van de wereld voor gebruik in de navigatie in een passende hervorming). Die kaart maakt hem wereldberoemd.
In het GeoGebraboek Mercator leer je meer over de achtergronden en de methode die Mercator gebruikte. Je ontdekt er dat Mercator geen onhandige cartograaf was die een hopeloos vervormde kaart ontwierp, maar een genie die het in zijn tijd moest uitzoeken zonder wiskundige kennis die voor ons nu vanzelfsprekend is.
why?
You can draw a map that looks as less distorted as possible, with areas that match or distances that match along certain lines. But why should one try to make true angle maps? The need for these kind of maps came from navigation because such maps are very useful. It's very practical if you siply can measure angles on a map to get the compass route to follow. But this was easier said than done.
Gerard Mercator succeeded in making such a world map in 1569 with his Nova et aucta orbis tarrae descriptio ad usum navigantium emendate accommodata (new and actual description of the world for use in navigation in a suitable reform). This map made him world famous.
In th GeoGebrabook Mercator you can learn more about the backgrounds and the methods Mercator used. You dicover that Mercator wasn't a clumsy cartographer who drew a hopeless distorted map, but a genius far ahead of his time who completed the job without the mathematics we're familiar with in our time.