ontvouwing van een cilinder
ontvouwing van ruimtelichamen met gebogen oppervlak
In de 3D knoppenbalk vind je wel een knop Ontvouwing 
, maar knop en commando Ontvouwing( ) werken enkel voor ruimtelichamen zonder gebogen zijvlakken. In een mooi staaltje programmeerwerk gebruikt Anthony Or parameteroppervlakken om ook van cilinders en kegels dynamische ontwikkelingen te creëren.
, maar knop en commando Ontvouwing( ) werken enkel voor ruimtelichamen zonder gebogen zijvlakken. In een mooi staaltje programmeerwerk gebruikt Anthony Or parameteroppervlakken om ook van cilinders en kegels dynamische ontwikkelingen te creëren. aanpak
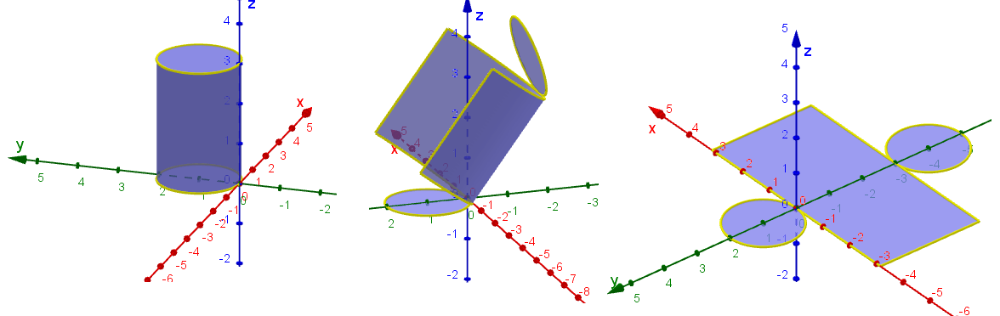
Een cilinder met straal 1 en hoogte 3 staat rakend aan de z-as met zijn grondvlak in het Oxy-vlak.
Tijdens de ontvouwing:
- blijft het grondvlak onveranderd in het Oxy-vlak.
- roteert de mantel 90° rond de rode x-as, tegelijk openplooiend tot een rechthoek.
- roteert het bovenvlak 180° t.o.v. de mantel zodat hij ook in het Oxy vlak terechtkomt.
mantel
De mantel wordt voorwaardelijk gedefinieerd als een parameteroppervlak.
Voor een parameteroppervlak definieer je achtereenvolgens de uitdrukkingen voor x, y en z, afhankelijk van twee parameters (hier u en v). De schuifknop t gaat van 0 tot 1.
Als(t < 1, Oppervlak(r sin(u θ), r (1 - cos(u θ)) cos(ϕ) - v sin(ϕ), v cos(ϕ) + r (1 - cos(u θ)) sin(ϕ), u, -1, 1, v, 0, 3), Oppervlak(π u, -v sin(ϕ), v cos(ϕ), u, -1, 1, v, 0, 3)).
Hierin is:
- t een schuifknop van 0 tot 1 die de ontvouwing stuurt. Deze factor t wordt ingebouwd in de hoeken en .
- = (1 - t) m.a.w een hoek die volgends de schuifknop t van tot 0 gaat.
- = t m.a.w. een hoek die volgens de schuifknop t van 0 tot gaat.
- r =
bovenvlak en ondervlak
Het bovenvlak wordt met het ingenest commando Roteer(Object,Hoek, Rotatieas) gedefinieerd als Roteer(Roteer(e, ϕ, a), ϕ, xAs). Hierin is a een rechte door (0,0,3) evenwijdig met de x-as.
Het bovenvlak wordt dus opengeplooid en tijdens dit openplooien roteert het mee met de mantel tot in het Oxy-vlak.
Het ondervlak is een cirkel die onverandert blijft.
Louter als visuele ondersteuning worden de omlijningen van mantel, onder- en bovenvlak extra gedefinieerd in een andere kleur.
In het algebravenster kan je de definities verkennen.
kegel
Op analoge manier creëert Anthony Or ook de ontwikkeling van een kegel.
Je vindt een werkblad op https://www.geogebra.org/m/ZcxuBrJ6.
Ben je geïnspireerd door de aanpak van de kegelontvouwing, download dan het applet en verken de definities in het algebravenster van het bestand.