Teorema de la base media
El segmento que une los puntos medios de dos lados de un triángulo:
- Es paralelo al tercer lado.
- Mide la mitad de la longitud del tercer lado.
Mueve los vértices del triángulo y comprueba el teorema
También, si del punto medio de un lado del triángulo se traza una paralela a otro lado:
- La paralela cortará al tercer lado en su punto medio.
- El segmento que une los puntos medios, medirá la mitad de la longitud del tercer lado.
Problema 1
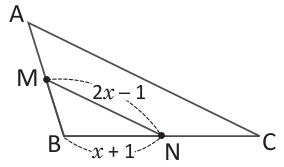
En el triángulo ABC, M y N son los puntos medios de AB y BC respectivamente. a) Calcula el valor de x, si BC = 8 cm. b) ¿Cuál es la longitud del lado CA?
Problema 2
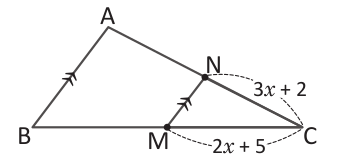
En el triángulo ABC, M es el punto medio de BC y NM AB. a) Calcula el valor de x si CA = 10. b) ¿Cuál es la longitud del lado BC?
Consecuencia del Teorema de la base media es el Teorema de Varignon, el cual dice:
Los segmentos que unen los puntos medios, de los lados consecutivos de cualquier cuadrilátero, siempre formarán un paralelogramo.
Mueve los vértices azules y comprueba el Teorema de Varignon. Marca las casillas para que veas la explicación.
Problema 3
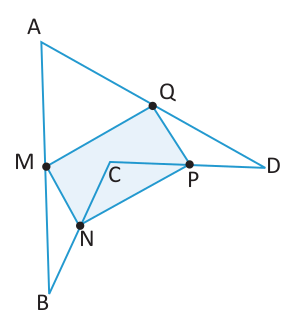
En el cuadrilátero ABCD, M, N, P y Q son los puntos medios de AB, BC, CD y DA respectivamente. Por tanto, el cuadrilátero MNPQ es un paralelogramo. Marca la 4 alternativas válidas, para demostrar que MNPQ es paralelogramo.