L6.8 - Equations and Graphs
Learning Intentions and Success Criteria
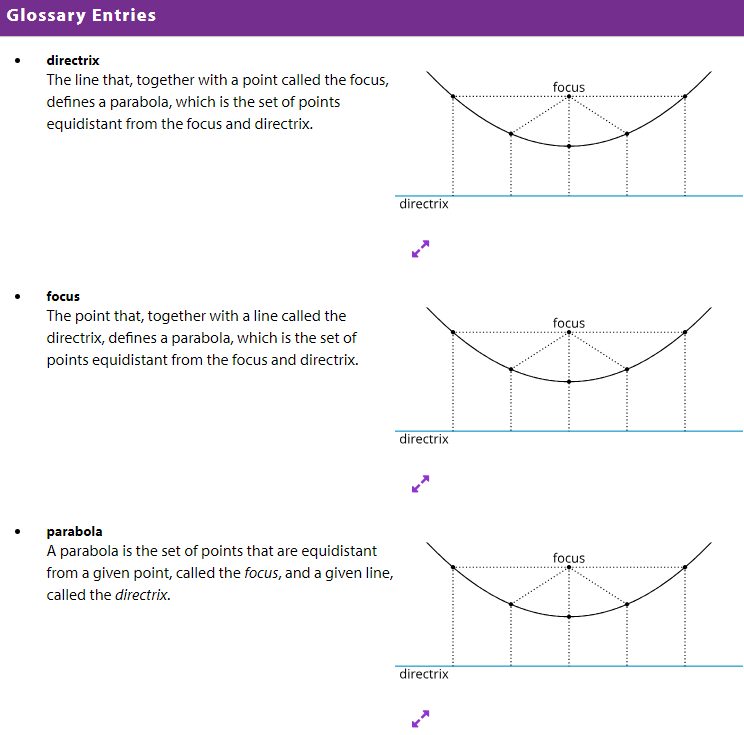
- Generalize (using words and other representations) the process of repeated distance calculations to derive an equation for a parabola in the coordinate plane.
- Derive an equation for a parabola in the coordinate plane given a focus and a directrix.
8.1: Focus on Distance
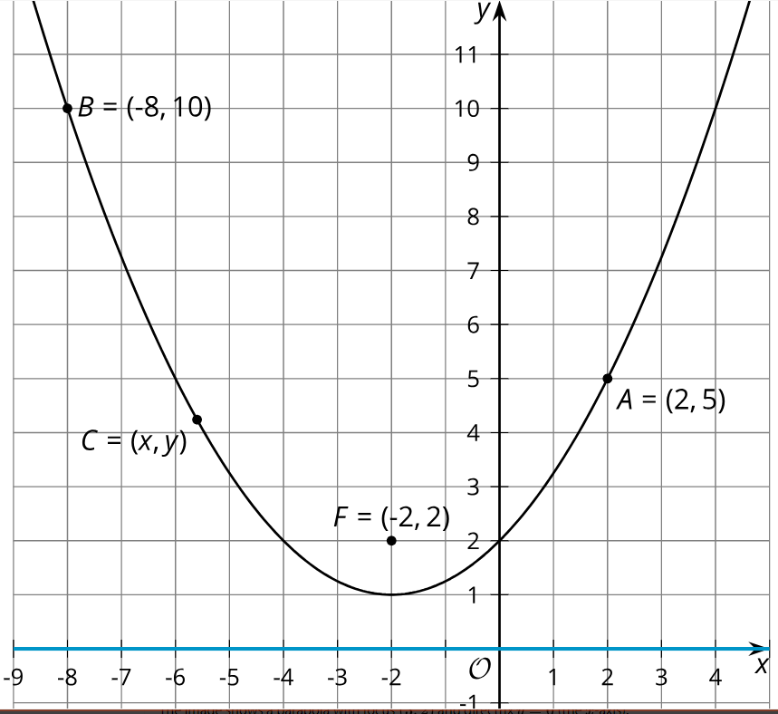
The image shows a parabola with focus (-2, 2) and directrix y = 0 (the x-axis). Points A, B, and C are on the parabola. Without using the Pythagorean Theorem, find the distance from each plotted point to the parabola’s focus. Explain your reasoning.
8.2: Building an Equation for a Parabola
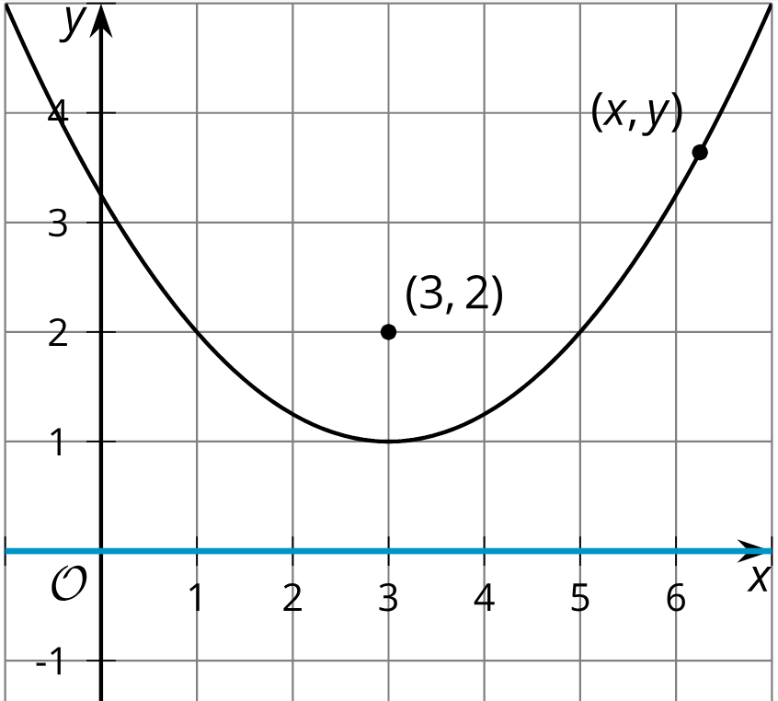
The image shows a parabola with focus (3, 2) and directrix y = 0 (the x-axis). 1. Write an equation that would allow you to test whether a particular point (x, y) is on the parabola.
2. The equation you wrote defines the parabola, but it’s not in a very easy-to-read form. Rewrite the equation to be in vertex form: y = a(x – h)2 + k, where (h, k) is the vertex.
8.3: Card Sort: Parabolas
Your teacher will give you a set of cards with graphs and equations of parabolas. Match each graph with the equation that represents it.
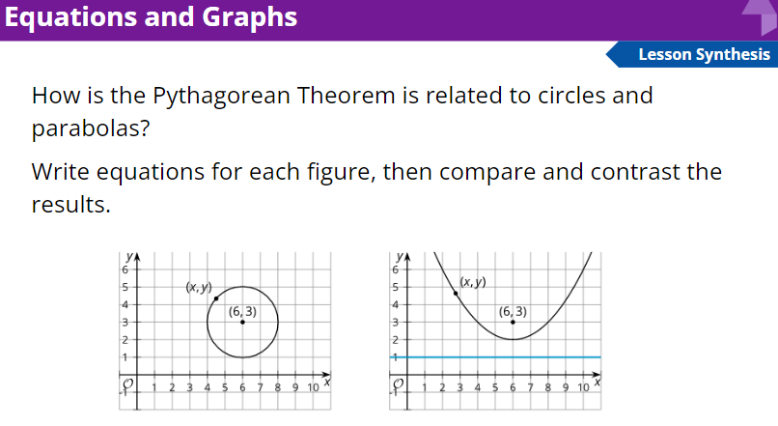
circle
parabola
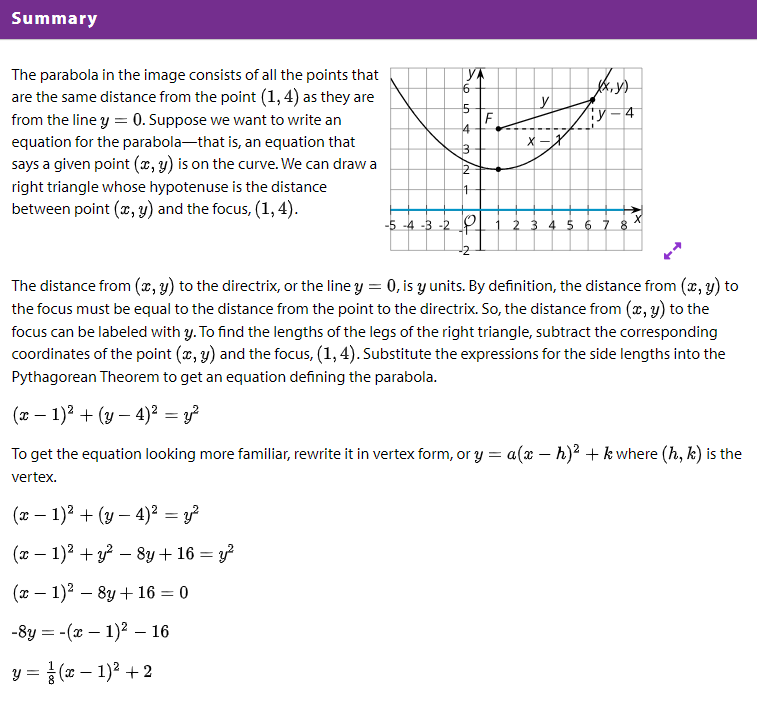
Learning Intentions and Success Criteria
- Generalize (using words and other representations) the process of repeated distance calculations to derive an equation for a parabola in the coordinate plane.
- Derive an equation for a parabola in the coordinate plane given a focus and a directrix.
Cool-Down: One More Equation
A parabola has focus (5, 7) and directrix y = 0 (the x-axis). Write an equation that says point (x, y) is on the parabola. You do not need to put it into vertex form. If it’s helpful, draw a sketch of the parabola.