Pythagorean Tiling
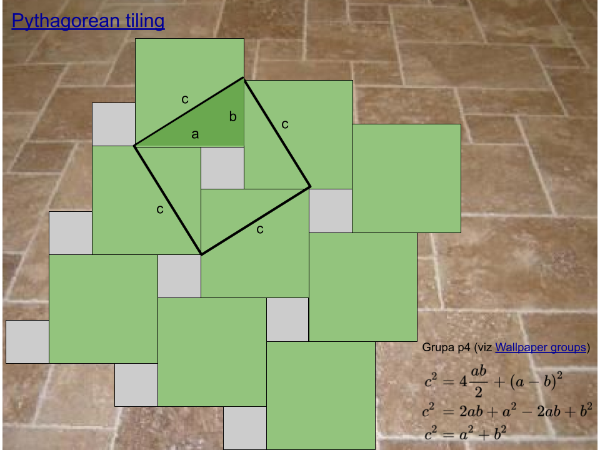
A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles.
Pythagorean tiling form a symmetric pattern from wallpaper group p4. The wallpaper group p4 has two rotation centres of order four (90°), and one rotation centre of order two (180°). It has no reflections or glide reflections.
Export for 3D print is available in GeoGebra 6 or web application. Use Settings (3 lines, up right corner) and export as stl file.
Model for 3D print
Puzzle, demonstration by Bhaskara II
![Cathedral of st. Vitus, [url=https://www.katedralasvatehovita.cz/flash/virtualni_prohlidka/index.html]virtual tour[/url], ([url=https://www.hrad.cz/en/prague-castle-for-visitors/virtual-tour]EN[/url])](https://beta.geogebra.org/resource/bm56cabr/Z4r0Ysxbt0yNt4c3/material-bm56cabr.png)
![Pavement in front of [url=https://cs.wikipedia.org/wiki/Gymn%C3%A1zium_Kladno]Gymnázium Kladno[/url].](https://beta.geogebra.org/resource/tprkxuet/duiDlOr5JIRochCe/material-tprkxuet.png)
