Ecuaciones Bicuadradas
1. Introducción
Una ecuación bicuadrada es una ecuación de la forma:
siendo .
Es, por tanto, una ecuación de cuarto grado en la que sólo tenemos los términos que tienen una potencia par de la incógnita. Como consecuencia, esta ecuación podrá tener, como mucho, 4 soluciones (reales) distintas.
Vamos a ver un método para la resolución de este tipo de ecuaciones y un par de ejemplos.
2. Método de Resolución
Existen diversos métodos para resolver las ecuaciones de grado mayor que 2, como la Regla de Ruffini. Pero el método que suele emplearse en las ecuaciones bicuadradas, por su simplicidad y rapidez, es aplicar el siguiente cambio de variable:
De este modo, al sustituir en la ecuación, obtenemos una ecuación de segundo grado:
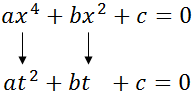
Resolvemos esta ecuación obteniendo dos soluciones: .
Deshacemos el cambio de variable (lo haremos para una de las soluciones):
Entonces,
Como tenemos dos soluciones (), obtendremos (hasta) 4 soluciones a la ecuación bicuadrada.
Notemos que si son negativas, entonces la ecuación bicuadrada no tiene soluciones (reales).
Resolvemos esta ecuación obteniendo dos soluciones: .
Deshacemos el cambio de variable (lo haremos para una de las soluciones):
Entonces,
Como tenemos dos soluciones (), obtendremos (hasta) 4 soluciones a la ecuación bicuadrada.
Notemos que si son negativas, entonces la ecuación bicuadrada no tiene soluciones (reales).
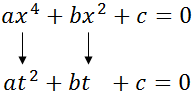
Resolvemos esta ecuación obteniendo dos soluciones: .
Deshacemos el cambio de variable (lo haremos para una de las soluciones):
Entonces,
Como tenemos dos soluciones (), obtendremos (hasta) 4 soluciones a la ecuación bicuadrada.
Notemos que si son negativas, entonces la ecuación bicuadrada no tiene soluciones (reales).
Resolvemos esta ecuación obteniendo dos soluciones: .
Deshacemos el cambio de variable (lo haremos para una de las soluciones):
Entonces,
Como tenemos dos soluciones (), obtendremos (hasta) 4 soluciones a la ecuación bicuadrada.
Notemos que si son negativas, entonces la ecuación bicuadrada no tiene soluciones (reales). 3. Ejemplos
Ejemplo 1

La ecuación de segundo grado resultante al aplicar el cambio de variable es
La ecuación de segundo grado resultante al aplicar el cambio de variable es
 cuyas soluciones son
cuyas soluciones son
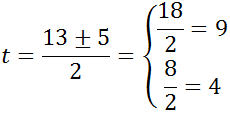 Ahora deshacemos el cambio de variable y tenemos las 4 soluciones distintas de la ecuación bicuadrada:
Ahora deshacemos el cambio de variable y tenemos las 4 soluciones distintas de la ecuación bicuadrada:
 Ejemplo 2
Ejemplo 2
 Por la forma de la ecuación, vamos a resolverla sin aplicar el cambio de variable. Usaremos el producto notable: suma por diferencia es igual a la diferencia de los cuadrados:
Por la forma de la ecuación, vamos a resolverla sin aplicar el cambio de variable. Usaremos el producto notable: suma por diferencia es igual a la diferencia de los cuadrados:
 Al tener la ecuación en forma factorizada, podemos deducir que las soluciones (son 3 soluciones distintas) son:
Al tener la ecuación en forma factorizada, podemos deducir que las soluciones (son 3 soluciones distintas) son:


La ecuación de segundo grado resultante al aplicar el cambio de variable es
La ecuación de segundo grado resultante al aplicar el cambio de variable es
 cuyas soluciones son
cuyas soluciones son
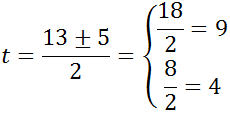 Ahora deshacemos el cambio de variable y tenemos las 4 soluciones distintas de la ecuación bicuadrada:
Ahora deshacemos el cambio de variable y tenemos las 4 soluciones distintas de la ecuación bicuadrada:
 Ejemplo 2
Ejemplo 2
 Por la forma de la ecuación, vamos a resolverla sin aplicar el cambio de variable. Usaremos el producto notable: suma por diferencia es igual a la diferencia de los cuadrados:
Por la forma de la ecuación, vamos a resolverla sin aplicar el cambio de variable. Usaremos el producto notable: suma por diferencia es igual a la diferencia de los cuadrados:
 Al tener la ecuación en forma factorizada, podemos deducir que las soluciones (son 3 soluciones distintas) son:
Al tener la ecuación en forma factorizada, podemos deducir que las soluciones (son 3 soluciones distintas) son:
