Construcción del Teorema de Viviani
El Teorema de Viviani (1622-1703) establece la siguiente propiedad de los triángulos equiláteros:
La suma de las perpendiculares a los lados desde cualquier punto de un triángulo equilátero es igual a la altura del triángulo
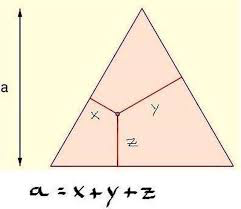
Aquí van las instrucciones de la Construcción
1. Crea un triángulo equilátero P con la herramienta "polígono regular"
2. Crea un punto D dentro de P con la herramienta "punto en objeto"
3. Con la herramienta "recta perpendicular" traza las rectas perpendiculares a los tres lados de P que pasen por D.
4. Calcula pos puntos de intersección E, F y G de esas rectas con los lados del triángulo P.
5. Crea los segmentos DE, DF y DG y calcula sus longitudes l, m y n con el comando Longitud(<objeto>).
6. Con el comando Distancia(<punto>,<objeto>) calculas la altura del triángulo y ya solo queda compararlo con la suma l+m+n.
Puede ver el resultado final en la siguiente applet:
En el siguiente Applet se construye paso a paso la demostración visual de este resultado, atribuida a K. Kawasaki en su artículo "Proof without words: Viviani's theorem", 2005.
Solo tienes que utilizar el deslizador para verla.