Activité : Le quadrilatère tournant
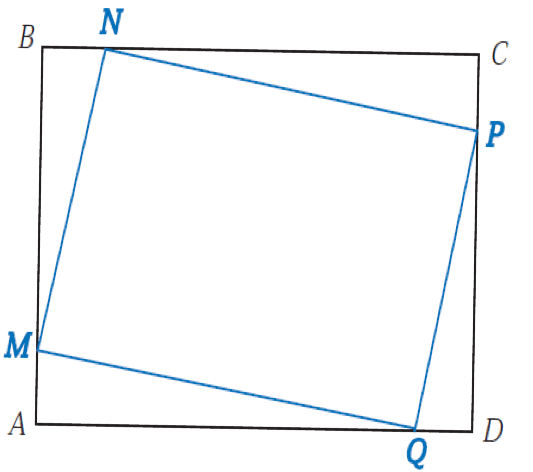
On considère un rectangle ABCD de dimensions données AB=6 cm et BC=8 cm.Sur le segment [AB], on place un point M quelconque.On place ensuite les points N sur [BC], P sur [CD] et Q sur [DA] tels que AM=BN=CP=DQ.
On s’intéresse à l’aire du quadrilatère MNPQ.
Partie 1
On propose de construire la figure avec le logiciel Geogebra.
- Faire afficher l’axe et la grille. Sélectionner Axe X :Axe Y, puis 1 :1. On obtient ainsi un repère orthonormé.
- Dans ce repère, placer
donner les coordonnées des points
et
. Placer alors les points
Tracer le rectangle
, pour cela tracer les segments du quadrilatère
- Créer un curseur comme indiqué ci-contre
- Placer le point
de coordonnées (0 ;a). Que représente ce curseur ?
- Déterminer les coordonnées de
et
en fonction de a. Placer les points
- Tracer le quadrilatère
en utilisant l’icône polygone :
- Faire afficher l’aire du quadrilatère
en utilisant l’icône
Partie 2
Conjecturer les réponses aux questions suivantes
Question 1
Où placer exactement le point M tel que l’aire du quadrilatère MNPQ soit égale à 25 cm² ?
Question 2
Comment varie l’aire du quadrilatère MNPQ ?
Question 3
Où placer exactement le point M pour que l’aire du quadrilatère soit strictement inférieure à 30 ?
Partie 3
Nous allons maintenant résoudre les 3 conjectures faites dans la partie 2. Pour cela à vous de choisir votre piste en fonction de vos capacités (à faire sur feuille).


