Multiplikation Ganzer Zahlen - Inhaltliche Deutung

Kurzinformation
- Thema: Multiplikation Ganzer Zahlen - Inhaltliche Deutung
- 7. Schulstufe, Mathematik
- Dauer: 2 Unterrichtseinheiten
- SchülerInnenmaterial
- LehrerInnenmaterial
Vorwissen und Voraussetzungen
Die SchülerInnen...
- ... haben ein inhaltliches Verständnis für den Zahlenbereich der ganzen Zahlen.
- ... können ganze Zahlen addieren und subtrahieren.
- ... haben ein inhaltliches Verständnis von diesen beiden Rechenoperationen.
Lernergebnisse und Kompetenzen
Die SchülerInnen ...
- ... kennen die Rechenregeln für die Multiplikation von ganzen Zahlen.
- ... kennen zwei verschiedene inhaltliche Deutungen für die Multiplikation von ganzen Zahlen. (Temperaturänderungen im Labor, Schulden)
Unterrichtsablauf
Die beiden Unterrichtseinheiten gliedern sich in drei Teile.
1. Einheit:
Teil 1: Die Schülerinnen bearbeiten ein Arbeitsblatt zum Thema Temperaturänderungen im Labor und dieses wird anschließend besprochen.
Teil 2: Mithilfe eines Tafelbildes werden die Rechenregeln für die Multiplikation von ganzen Zahlen besprochen und bearbeitet.
2. Einheit:
Teil 3: Die Schülerinnen lernen mithilfe des Schuldscheinspiels einen neuen Kontext zur Multiplikation von ganzen Zahlen kennen und führen während des Spiels ein Protokoll.
Arbeitsblatt Temperaturänderungen im Labor (30 min)
Die Schülerinnen bekommen das ArbeitsblattTemperaturänderungen im Labor und sollen dieses zuerst in Einzelarbeit bearbeiten. (20 min)
Anschließend werden die Lösungen und Erkenntnisse im Plenum mit der Lehrperson besprochen. (10 min)
Dabei sollte die Lehrperson explizit auf die zwei wichtigen Erkenntnisse aufmerksam machen.
Für positive Zahlen a und b gilt: a · (-b) = - (a · b)
Für positive Zahlen a und b gilt (-a) · (-b) = a · b
Rechenregeln für die Multiplikation (20 min)
Die Lehrperson gibt mithilfe eines Tafelbildes zuerst die allgemeine Definition der Rechenregeln für die Multiplikation ganzer Zahlen. Anschließend wird diese Definition mittels bereits bekannter Rechenregeln gerechtfertigt.
Tafelbild
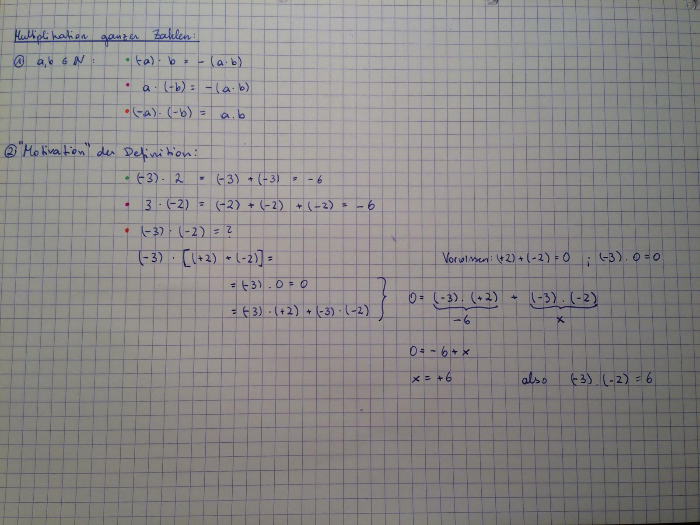
Das Schuldscheinspiel (50 min)
Mithilfe des Schuldscheinspielssollen die Schülerinnen spielerisch einen neuen Kontext für die Multiplikation von ganzen Zahlen kennen lernen. Die Schüler erhalten dazu ein Anweisungsblatt um einen geregelten Spielverlauf zu erreichen.
Vorbereitung:
Man benötigt eine Schülerin oder einen Schüler, der den Bankhalter spielt. Dieser erhält
Schuldscheine und Gutscheine von je 50€ Wert. Des Weiteren bereitet man zwei
Urnen vor. In der ersten befinden sich 10 grüne Zettel mit der Aufschrift „+1
bis +10“, 10 rote Zettel mit der Aufschrift „-1 bis -10“ sowie ein weißer Zettel
mit der Aufschrift „0“. In der zweiten Urne befinden sich zwei Zettel, einer
mit der Aufschrift „50€ Gutschrift“ und die andere mit der Aufschrift „50€
Lastschrift“.
Druckvorlage
Spielablauf:
Es wird in Gruppen von
jeweils 3 Schülerinnen gespielt. (1 Bankhalter und 2 Spieler)
Beide Spieler starten mit einem ausgeglichenen Konto,
der Kontostand beträgt also 0€. Abwechselnd kann nun jeder je einen Zettel aus
beiden Urnen ziehen, welche wieder zurückgemischt werden müssen.
Folgendes wird sich dann beispielsweise ergeben:
(+3) · (+50€)
Du bekommst (vom Bankhalter) 3 Gutscheine von je 50€, du wirst um 150€ reicher.
(-3) · (+50€)
Du gibst 3 Gutscheine von je 50€ (an den Bankhalter) ab, du wirst um 150€ ärmer.
(+3) · (-50€)
Du bekommst (vom Bankhalter) 3 Schuldscheine von je 50€, du wirst um 150€ ärmer.
(-3) · (-50€)
Du gibst 3 Schuldscheine von je 50€ (an den Bankhalter) ab, du wirst um 150€ reicher.
Wer nun nach 15 Spielzügen am meisten Geld hat, hat gewonnen.
Wer zufällig noch keine Scheine hat aber welche abgeben muss, muss sich vom Bankhalter welche geben lassen.
Dabei gilt aber die „Entgegengesetztheit“. Er bekommt in der Anzahl gleich
viele Schuld- und Gutscheine, z.B.: (+3) · (+50€) + (+3) · (-50€) = 0
Überprüfen des Lernerfolges
In der ersten Unterrichtseinheit erfolgt die Überprüfung des Lernerfolges während der Besprechung der Lösungen und Erkenntnisse im Plenum. Zusätzlich können die Arbeitsblätter abgesammelt und kontrolliert werden.
Am Ende der Unterrichtseinheit wird zur Überprüfung von jedem Schüler das Spielprotokoll abgesammelt.
Quellen
Mathematik verstehen 3, Schulbuch; Salzger, Bernhard; Bachmann, Judith; Germ, Andrea; Riedler, Barbara; Singer, Klaudia; Ulovec, Andreas
Skript „Von den natürlichen Zahlen über die Bruchzahlen zu den rationalen Zahlen“, Humboldt-Universität zu Berlin
http://didaktik.mathematik.hu-berlin.de/files/skript_radermacher.pdf
Mathematik Lehren, "Ein Kontext für negative Zahlen auch für die Multiplikation",183, 2014