VOLUMEN DE SÓLIDOS EN REVOLUCIÓN
Actividad diagnóstica
Como es sabido de todos ustedes, antes de iniciar con el tema que nos ocupará, debemos retomar algunos conocimientos que ya están en nuestro archivo de conocimientos y que nos permitirán construir nuevos y significativos aprendizajes, partiendo de lo que ya sabemos.
Para ésta ocasión, los conocimientos previos que debemos retomar son aquellos que tienen que ver con el volumen de cuerpos tridimensionales.
Pero tampoco se trata de volver a tomar toda la clase de geometría de cuerpos tridimensionales, sólamente retomaremos el concepto de volumen y recordaremos ls fórmulas para calcular el volumen de algunos cuerpos, específicamente de los prismas rectangulares y los prismas cilíndricos.
Entendemos por VOLUMEN "La región de espacio que limita el área de un poliedro", entendiendo por POLIEDRO "Un cuerpo geométrico al que limitan polígonos" (CONAMAT. 2015. Matemáticas Simplificadas. Cuarta Edición. p 767. Editorial PEARSON. México, D.F.).
Entonces un prisma rectangular es un poliedro, ya que es un cuerpo geométrico limitado por polígonos.
A continuación una representación de un prisma rectangular:
Un prisma rectangular tiene una base de dimensiones b X a y una altura h. Para obtener su volumen de un prisma, se debe calcular el área de su base y multiplicarla por la altura. Así entonces, para calcular el área de un prisma rectangular se obtiene el área de la base y se multiplica por la altura de la siguiente forma:
Un prisma rectangular tiene una base de dimensiones b X a y una altura h. Para obtener su volumen de un prisma, se debe calcular el área de su base y multiplicarla por la altura. Así entonces, para calcular el área de un prisma rectangular se obtiene el área de la base y se multiplica por la altura de la siguiente forma:
A manera de ejemplo, si un prisma rectangular tiene las siguientes dimensiones:
cm
cm
cm
Entonces su volumen se calcula por:
cm3
Como podemos observar, no es un cálculo que sea muy complicado.
Veamos ahora un prisma circular, al que llamamos cilindro:
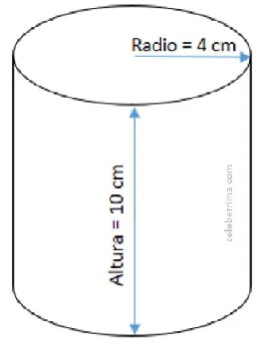
Como podemos observar en la figura, tenemos básicamente dos medidas principales en un prisma circular: El radio y la altura.
Para el cálculo de su volumen, nuevamente hay que obtener primeramente el área de la base y después multiplicarlo por su altura de la siguiente manera:
Así pues, el volumen del cilindro mostrado en la figura se calcula así:
cm2
Es necesario hacer no perder de vista que las figuras tridimensionales está perfectamente delimitadas en todas sus fronteras por figuras geométricas.
Una vez que recordamos éstos conocimientos, podemos empezar el estudio del tema que nos ocupará: Volumen de Sólidos en Revolución.
SÓLIDOS EN REVOLUCIÓN
¿Qué se debe entender por la expresión Sólido en Revolución?
Es un poco complicado de visualizar, pero debemos abrir nuestra imaginación y visualizar en nuestra mente la siguiente situación:
Supongamos que tenemos la gráfica de la siguiente función:
Como podemos ver, se trata sencillamente de una línea recta a 45° de la horizontal. Nada nuevo para nosotros pues ya cursamos muchas asignaturas donde estudiamos líneas rectas y sus gráficas.
Sin embargo, ahora le vamos a dar, literalmente, un giro a nuestra imaginación. Vamos a hacer que la línea gire alrededor del eje de las abscisas (eje "x), por lo que obtendremos dos figuras cónicas con vértice en el origen del plano cartesiano de la siguiente manera:
De esa forma, hemos generado un Sólido en Revolución.
Entonces, un sólido en revolución "se genera al hacer girar un área plana en torno de una recta conocida como eje de rotación o eje de revolución" (CONAMAT. 2015. Matemáticas simplificadas. Cuarta Edición, p 1406. Editorial PEARSON. México, D.F.)
Un ejemplo de esto son los artesanos que moldean el barro haciendo girar un disco y le dan forma a un cúmulo de barro que colocan sobre él. Sin saberlo, están generando un sólido en revolución.
Imagen tomada de la página web https://tlaquepaque.artesano.tour.gdltours.com/blog/
Imagen tomada de la página web https://tlaquepaque.artesano.tour.gdltours.com/blog/VOLUMEN DE UN SÓLIDO EN REVOLUCIÓN
La figura del cono fue seleccionada deliberadamente porque es muy fácil visualizar el cálculo de su volumen.
Para calcular el volumen de un sólido en revolución nuevamente debemos abrir nuestra imaginación y retomar la imagen de los conos giratorios que generamos en el plano cartesiano.
Ahora que ya está visualizada la imagen de los conos en el plano cartesiano, pretendemos calcular su volumen.
Al igual que lo hicimos al calcular el área bajo la curva usando los rectángulos, ahora vamos a calcular el volumen de los conos usando cilindros infinitesimalmente delgados, cortados transversalmente como "rebanadas" dentro de dos límites establecidos [a, b] donde a es límite inferior y b es el límite superior.
Entonces debemos calcular el volumen de una cantidad infinita de cilindros que tienen un radio y un ancho que haremos tender hacia 0.
Pero, ¿Cuánto miden el radio y el ancho? Muy sencillo. El radio mide f(x) y el ancho mide dx, de tal manera que el cálculo de volumen de cada cilindro estará definido por la expresión:
Como el volumen de cada "rebanada" de cilindro forma parte de un volumen total, podemos decir que, individualmente, son un diferencial de volumen, por lo que se han designado como dV.
Así, al calcular la sumatoria del volumen de todos los discos o "rebanadas", se calcula una integral, en donde dx se hace tender a 0 y obtenemos la siguiente expresión:
pero, como sabemos es una constante y, por lo tanto, podemos sacarlo de la integral y nuestra expresión final para el cálculo de volúmenes de sólidos en revolución queda determinado por la siguiente integral:
EJEMPLO
A manera de ejemplo, calcularemos el área del cono generado por la recta propuesta dentro de los límites y
Tenemos entonces
u2
Calculemos ahora el volumen de un cono con diámetro 2 pulg y altura 2 pulg usando la fórmula del volumen de un cono para comparar nuestros resultados:
pulg2
Con lo que comprobamos que el cálculo por integrales es idéntico al cálculo del volumen por geometría.
Para seguir resolviendo ejemplos a detalle, calcularemos ahora el volumen de un jarrón de metal que será producido en serie mediante torno seguidor, y que su contorno interno seguirá la forma de la siguiente función:
con límite inferior y superior
Ahora que ya tenemos visualizada la figura del jarrón que se desea producir, procedemos a calcular el volumen que tendrá dicho jarrón. Las unidades están en metros, por lo que es un jarrón decorativo bastante grande.
Para resolver la integral de manera más sencilla, primero se debe desarrollar el trinomio al cuadrado que tenemos:
Reduciendo términos semejantes tenemos
Ahora sí podemos integrar fácilmente
m3
Es decir, al jarrón le caben casi 4,000 litros.
SOLO PARA PRACTICAR
Calcula el volumen de un silbato de juguete en forma de trompeta que sigue el contorno de la función
con límite inferior y límite superior . Todas las medidas están en cm.
SUGERENCIA: Integra utilizando el método de cambio de variable haciendo
RESPUESTA: cm3