Drone Data
Antidote Testing Data
We have been testing different antidotes for the radiation pollution.
The following graph about the first antidote we created, shows the rate at which it removes radiation from the atmosphere, it models a negative quadratic function.
Analysing the graph:
What are the coordinates of the y-intercept?
What does this mean? (Considering the first data point is at the beginning before any days have passed with the antidote present)
Millisieverts - Radiation level readings
Millisieverts (mSv) are a unit of measure for radiation levels.
1000 mSv is a dangerous level for living beings, it can cause sickness but that level of radiation would not be fatal.
100 mSv is the lowest annual dose which can cause health problems so still not ideal but we are aiming to reduce the levels to below 100.
The data models a quadratic function with the equation y=1000-25x
Complete the following table of values to find coordinates of some of the points on the graph:
Example:
1=1
1x25=25
1000-25=975
After how many days will the radiation levels fall below 100 mSv?
Use the slider to see what happens when you increase or decrease m (the coefficient of x squared)
Write down what you notice, do we want the coefficient of x squared to be more than -25 or less than -25?
What is the drop in mSv between day 2 and day 4?
We have been running further tests on this antidote and the 6 outcomes are shown in the results below. There was a mix-up though with this data. Can you match each graph with the correct quadratic equation?
The equations are:
y=1000-2x2
y=1000-5x2
y=1000-10x2
y=1000-25x2
y=1000-50x2
y=1000-100x2
Antidote A
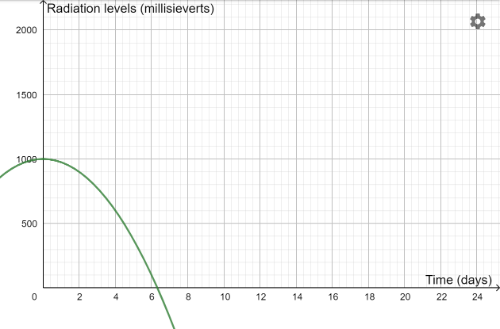
Antidote B
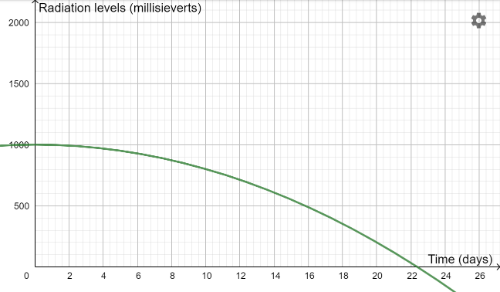
Antidote C
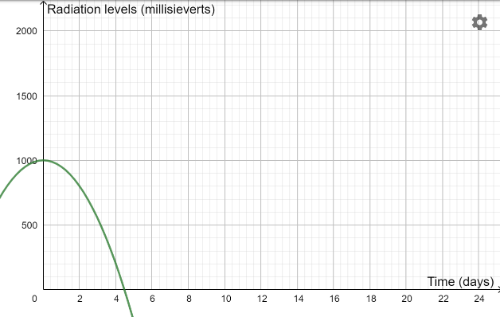
Antidote D
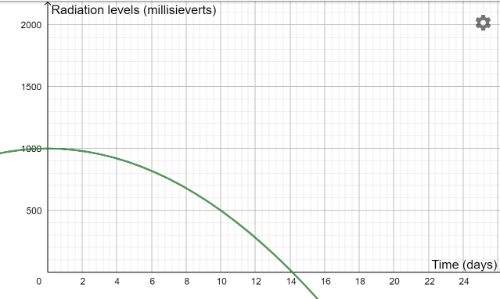
Antidote E
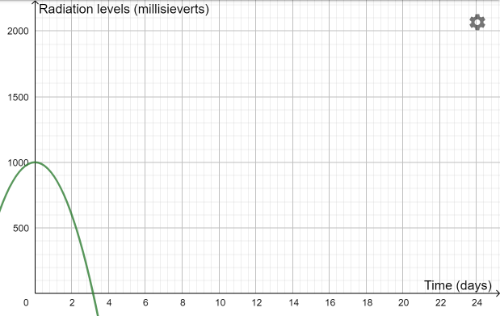
Antidote F
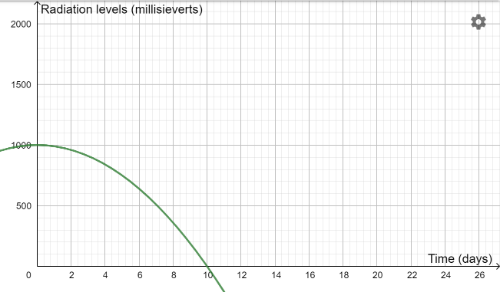
Can you match each antidote with an equation? Here is a reminder of the equations: y=1000-2x2 y=1000-5x2 y=1000-10x2 y=1000-25x2 y=1000-50x2 y=1000-100x2
Which antidote would be the most successful trial, and the one we should select to use in the town?