Le rette e i sistemi lineari
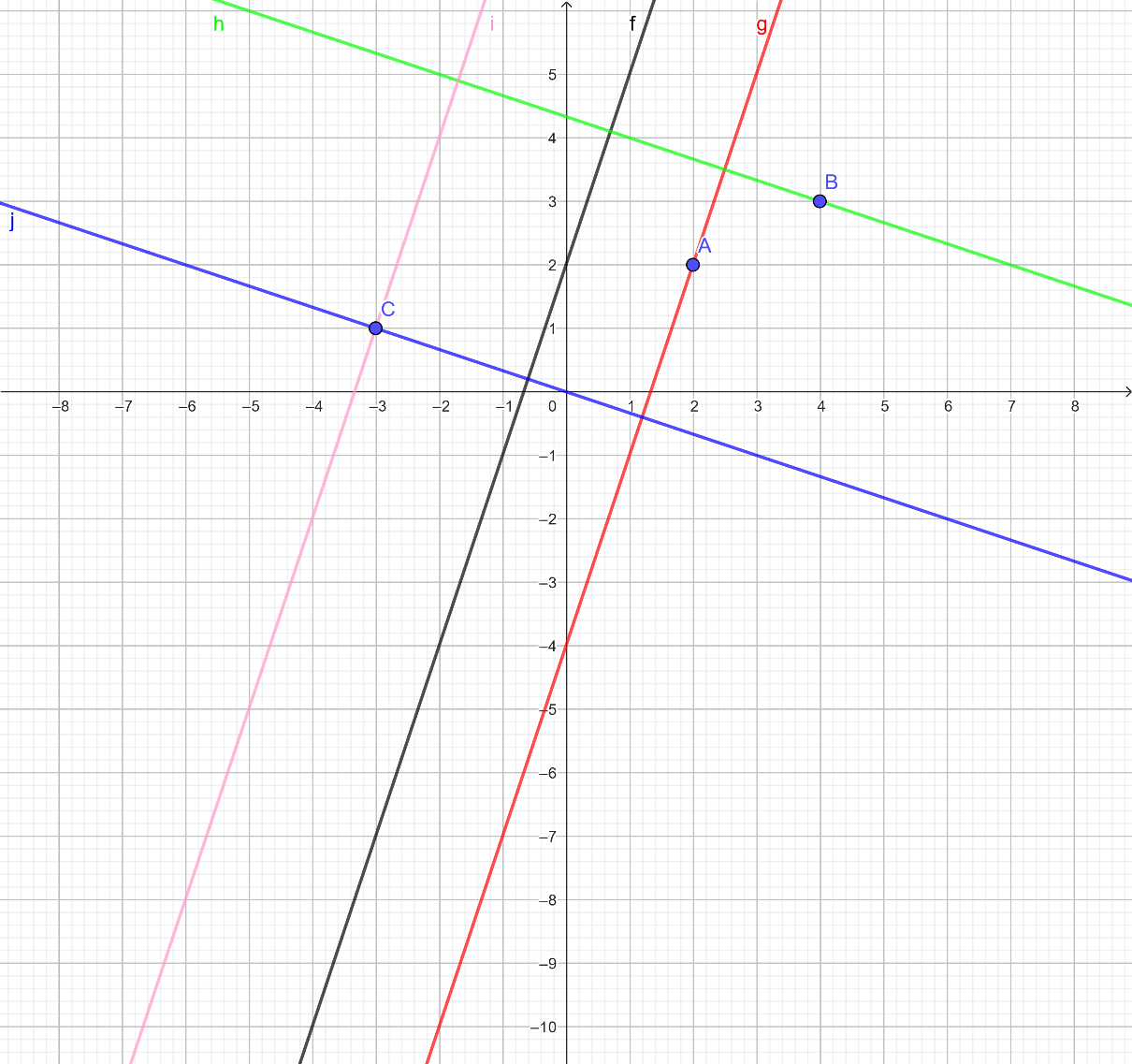
Rispondi alle seguenti domande. In allegato trovate l'immagine di come deve risultare il grafico,
Prima domanda: Trasforma l'equazione della retta del punto 1) in forma implicita e scrivi i valori dei coefficienti a,b,c. Seconda domanda: scrivi i valori di m (cioè del coefficiente angolare) e i valori di q delle rette trovate nei punti 3) e 4). Terza domanda: quale relazione esiste fra i coefficienti angolari (cioè m) di una retta e della sua paralella? Quarta domanda: quale relazione esiste fra i coefficienti angolari (cioè m) di una retta e della sua perpendicolare? Quinta domanda: dopo aver trasformato le rette dei punti 3) e 4) in forma implicita, scrivi i valori di a, b, c di entrambe le rette. Sesta domanda: le equazioni delle due rette paralelle alla prima in cosa differiscono? Settima domada: noi conosciamo le coordinate del punto C, (-3,1). Da un punto di vista algebrico, cosa rappresentano queste coordinate? Ottava domanda: determina algebricamente (ovvero facendo i calcoli) le coordinate del punto. (Risolvi il sistema lineare che si forma con le equazioni delle due rette dei punti 5) e 6) con uno dei quattro metodi....)