Outline
Bizentrische 4-Ecke
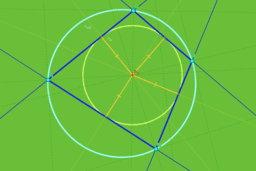
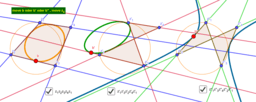
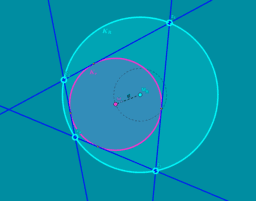
- 4 Punkte auf einem Kreis kann man ein Kreis-4-Eck nennen. Der Kreis ist dann der "Umkreis" des 4-Ecks. Meist besitzt ein 4-Eck keinen Umkreis!
- Berühren 4 Seiten eines 4-Ecks einen Kreis, so spricht man von einem Kreis-Tangenten-4-Eck.
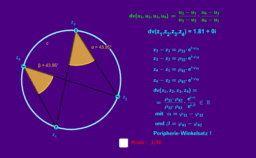
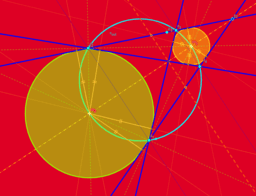
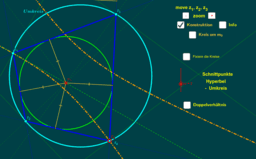
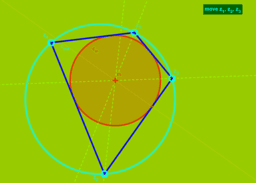
- Ein 4-Eck, welches sowohl ein Kreis-4-Eck, als auch ein Kreis-Tangenten-4-Eck ist, wird bizentrisch genannt. Zentren sind die beiden Kreismittelpunkte.
- Unter welchen Bedingungen ist ein 4-Eck bizentrisch?
- Welche Eigenschaften besitzen bizentrische 4-Ecke?
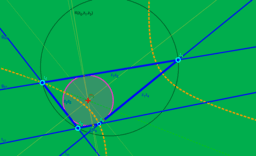
- Wie konstruiert man bizentrische 4-Ecke?
- Welche Symmetrieen gibt es?
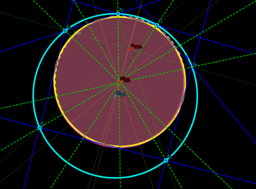
- Wieviele Berührkreise kann es geben? (3-Ecke besitzen 1 Inkreis und 3 Ankreise!)