L5.4 - Scaling and Area

Auteur:Ms. Leon-Guerrero (Ms. LG)

Onderwerp:Oppervlakte, Dilatatie, Lichamen

Learning Intentions and Success Criteria

We are learning to:

Comprehend that when figures are dilated by a scale factor of k, their areas are multiplied by k².

We are successful when we can:

Know that when figures are dilated by a scale factor of k, their areas are multiplied by k².

Approximately symbol ≈

4.1: Squares and Roots

1. What number times itself equals 25?

2. What number times itself equals 81?

3. What number times itself equals 10?

4.2: Scaling Up a Rectangle

Here is a rectangle with length 5 units and width 2 units.

1. What is the area of the rectangle?

2. Dilate rectangle ABCD from point A by a scale factor of 2. Calculate the area of the image.

3. Dilate rectangle ABCD from point A by a scale factor of 3. Calculate the area of the image.

4. Complete the table.

5. Write an expression for the area of a rectangle with length l and width w.

6. Imagine dilating the rectangle with length l and width w by a factor of k. Write expressions for the dimensions of the dilated rectangle.

7. Write an expression for the area of the dilated rectangle.

8. Use your work to draw a conclusion about what happens to the area of a rectangle when it’s dilated by a scale factor of k.

4.3: What About Other Shapes?

Andre says, “We know that if a rectangle is scaled by a factor of k, the area scales by a factor of k². Does this apply to other shapes?” Jada says, “Here’s a shape that’s not a rectangle. Say its area is A square units. Let’s draw some rectangles on it that get smaller and smaller to fit the remaining empty space. With enough rectangles we can come close to covering the whole blob.”

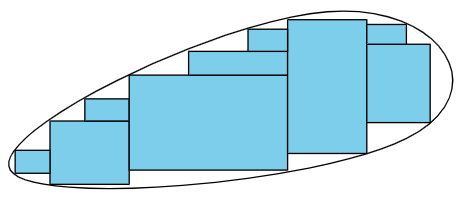
Andre says, “These rectangles start to make a nice approximation of the blob. If we wanted to get closer, we could add even more rectangles. The sum of the areas of all the rectangles would add up to the area of the blob. I think we’re almost there!” 1. Suppose the blob is dilated by a factor of k. In doing this, the rectangles covering the blob also get dilated by a factor of k. How does the area of each dilated rectangle compare to the area of each original rectangle?

2. What does this tell you about the area of the dilated image? Explain your reasoning.

3. Suppose a circle has area 20 square inches and it’s dilated using a scale factor of 6. What is the area of the image? Explain or show your reasoning.