El criterio de congruencia LAL
Los ángulos también ayudan
¿Ya ha quedado claro el criterio LLL? Si es así, entonces es momento de pasar a otra cosa; si no, te sugerimos revisar de nuevo la hoja anterior y acercarte a tu profesor para que te ayuda a aclarar las dudas.
Hasta el momento sólo nos hemos fijado en la medida de los lados de dos triángulos para determinar si son congruentes o no. ¿Y qué hay de los ángulos internos de un triángulo? Pues resulta que son otro elemento que puede ayudarnos a saber si existe congruencia o no. Revisa el siguiente video desde el inicio hasta el minuto 1:39 para comenzar a familiarizarte con el tema:
Recuerda: desde el inicio hasta el minuto 1:39
¿Qué tal, ya es más o menos claro cómo utilizar este criterio? Si no vamos a hacer un pequeño ejercicio. Considera los triángulos ABC y FDE dibujados abajo. Como puedes ver, estos triángulos tienen dos ángulos idénticos (ojo: de los otros dos ángulos no podemos decir nada en este momento). Ahora utiliza la herramienta Distancia  para medir los lados que forman cada uno de esos ángulos. Nota: no arrastres ningún punto en este momento.
para medir los lados que forman cada uno de esos ángulos. Nota: no arrastres ningún punto en este momento.
 para medir los lados que forman cada uno de esos ángulos. Nota: no arrastres ningún punto en este momento.
para medir los lados que forman cada uno de esos ángulos. Nota: no arrastres ningún punto en este momento.¿Qué pasa con esta magnitudes?
¿Los lados AC y FE miden lo mismo?
¿Los lados BC y DE miden lo mismo?
De manera que tenemos dos triángulos que, como señala el video, tienen dos lados iguales y también el ángulo que forman dichos lados es igual...¡esas son las condiciones del criterio de congruencia LAL! Esto nos lleva a pensar...¿qué debe ocurrir con el tercer lado? ¡Comprueba tu hipótesis usando nuevamente la herramienta Distancia  ! Mide los lados AB y DF en ambos triángulos y compara las magnitudes.
! Mide los lados AB y DF en ambos triángulos y compara las magnitudes.
 ! Mide los lados AB y DF en ambos triángulos y compara las magnitudes.
! Mide los lados AB y DF en ambos triángulos y compara las magnitudes.A partir de comparar esas magnitudes responde...
¿Son esos triángulos congruentes?
La siguiente imagen ilustra de manera general el criterio LAL
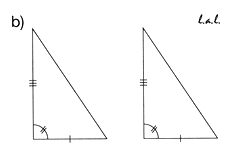
¡Ahora te toca a ti!
Es momento de que pongas manos a la obra para practicar un poco. Debes construir un triángulo congruente al que ya está dibujado teniendo en mente el criterio LAL. Para tener un punto de partida te hemos dado un par de rectas que forman un ángulo idéntico a uno de los triángulos. Sugerencia: utiliza las herramientas Compás  y Segmento
y Segmento  para tu construcción. Después utiliza la herramienta Distancia
para tu construcción. Después utiliza la herramienta Distancia  para medir los lados de cada triángulo y luegoarrastra cualquier punto para verificar que los triángulos siguen siendo congruentes.
para medir los lados de cada triángulo y luegoarrastra cualquier punto para verificar que los triángulos siguen siendo congruentes.
 y Segmento
y Segmento  para tu construcción. Después utiliza la herramienta Distancia
para tu construcción. Después utiliza la herramienta Distancia  para medir los lados de cada triángulo y luegoarrastra cualquier punto para verificar que los triángulos siguen siendo congruentes.
para medir los lados de cada triángulo y luegoarrastra cualquier punto para verificar que los triángulos siguen siendo congruentes.