Suma de los ángulos interiores de un triángulo - Lección 01-04
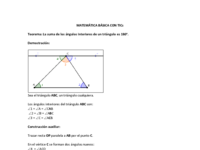
Teorema: La suma de los ángulos interiores de un triángulo es 180°.
Los vértices de un triángulo normalmente se identifican con letras mayúsculas.
En el applet que se muestra a continuación los vértices del triángulo son ABC.
Los ángulos interiores de un triángulo se pueden identificar de varias formas como se muestra en el applet:
- Ángulo A = Ángulo CAB = Ángulo 1
- Ángulo B = Ángulo ABC = Ángulo 2
- Ángulo C = Ángulo BCA = Ángulo 3.
También se pueden utilizar letras griegas, , , , etc.
Actividades:
1. Active la animación del applet siguiente (botón Iniciar animación) para visualizar que la suma de los tres ángulos del triángulo suman 180°.
La animación utiliza tres deslizadores t1, t2 y t3 que se activan en forma consecutiva pero cada deslizador se puede manipular en forma independiente.
Para modificar el triángulo utilice los puntos A, B y C.
2. Analice la demostración del teorema que se muestra en el archivo pdf.
Suma de angulos del triangulo - demostración
3. En el triángulo MNP el ángulo M mide 60° y el ángulo P mide 45°. Cuál es la medida del ángulo N.
4. El triángulo PQR es rectángulo en Q y además es isósceles. La medida de los ángulos del triángulo son:
En la figura se tienen las siguientes medidas de los ángulos:
1 = 50°
3 = 75°
6 = 25°
9 = 60°
Además, los ángulos BAE y ABC son rectos.
Responda las preguntas 5, 6, 7 y 8:
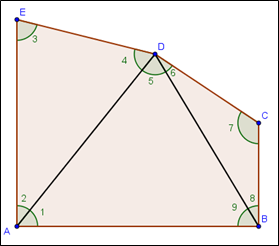
5. Determine la medida del ángulo 4.
6. Determine la medida del ángulo 5.
7. Determine la medida del ángulo 8:
8. Determine la medida del ángulo 7:
Otras tareas.
Abra la actividad Ángulos en el triángulo, https://www.geogebra.org/m/kgbmbv2v.
a) Utilice el applet No. 2, dibuje un triángulo cualquiera y compruebe el teorema de la suma de los ángulos del triángulo por recortado.
a) Utilice el applet No. 3, dibuje un triángulo cualquiera y compruebe el teorema de la suma de los ángulos del triángulo por plegado.