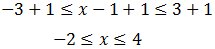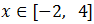Inecuaciones con Valor Absoluto
1. Introducción
El valor absoluto de un número a, representado como |a|, es su valor numérico (con signo positivo).
Por ejemplo,
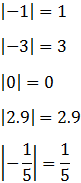
Notemos que:
Notemos que:
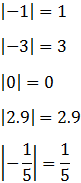
Notemos que:
Notemos que: - si el número es positivo, su valor absoluto es el propio número;
- si el número es negativo, su valor absoluto es su opuesto (número con signo opuesto, es decir, con signo positivo);
- si el número es 0, su valor absoluto es 0, aunque 0 no es ni positivo ni negativo.
- si tenemos la desigualdad (menor o igual) podemos escribir
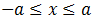
que es lo mismo que decir
que es lo mismo que decir
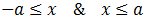
O bien, usando intervalos:
O bien, usando intervalos:
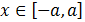
- si tenemos la desigualdad (mayor o igual) podemos escribir
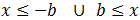
O bien, usando intervalos:
O bien, usando intervalos:
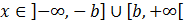
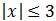
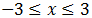
Por tanto, la solución es
Por tanto, la solución es
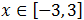
Ejemplo 2:
Ejemplo 2:
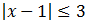
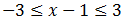
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:
Sumamos 1:
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:
Sumamos 1: